Příklady pro výpočet plošného obsahu tělesa (povrchu tělesa) - poslední strana
Počet nalezených příkladů: 976
- Vypočítejte S,V koule
Vypočítejte povrch a objem koule o poloměru 3m. - Polomer 81822
Výška a polomer valca jsou 25 stôp a 5 stôp. Jaký je povrch valca? - (1/3)*PI*h*h*(3R-h) 82080
Mám stan ve tvaru kulové čepice (kulový odstavec). Předpokládejme, že chceme, aby objem byl 4 metry krychlové, aby se tam vyspali dva nebo tři lidé. Předpokládejme, že materiál tvořící kopuli desítky je dvakrát dražší na čtverec než materiál dotýkající se - Zdvojnásobení objemu
Vytvořte si novou plechovku od nápoje, která zdvojnásobí objem použité původní plechovky. Rozměry dózy: průměr 6 cm a výška 10 cm. Máte zdvojnásobit objem s co nejmenším množstvím dodatečného hliníku potřebného pro novou plechovku. Jsou 3 možnosti: Možnos
- Trojúhelníkových 81540
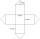Frank navrhl síť pro skladovací prostor, který se chystá postavit z kovu. Design se skládá ze čtvercové základny a čtyř čtverečních stran plus čtyř trojúhelníkových částí, které tvoří střechu. Čtvercová základna 6 stop a čtyři čtvercové strany plus 4 stop - Přibližné 81700
Pekárna vyrábí válcové mini muffiny, které měří 2 palce v průměru a 1 a 1/4 palce na výšku. Pokud je každý mini muffin zcela zabalen v papíře, tak alespoň kolik papíru je potřeba k zabalení 6 mini muffinů? Přibližné použití pi se rovná 22 na 7. - Vypočítejte 82152
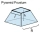Seříznutý jehlan se skládá ze čtvercové základny o délce 10 cm a vrchního čtverce o délce 7 cm. Výška seříznutého jehlanu je 6 cm. Vypočítejte povrch a objem. - Seříznutého 82013
Stínítko lampy jako komolý má výšku 12 cm a horní a dolní průměr 10 cm a 20 cm. Jaká plocha materiálů je potřebná k pokrytí zakřiveného povrchu seříznutého okraje? - Vysvětlete 81386
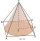Kužel má průměr x cm a výšku sklonu y cm. Čtvercový jehlan má délku strany základny x cm a výšku sklonu y cm. Který má větší povrch tělesa? Vysvětlete.
- Zmenší + zvětší
Poloměr plného kruhového válce se zmenší o 20 % a jeho výška se zvětší o 10 %. Najděte procentuální změnu: a) objemu b) povrch zakřivené části pláště. - Výsledný kvádr
Dvě kostky každá o objemu 125 cm³ jsou spojeny konci. Najděte povrch výsledného kvádru. - Kostka 4
Kostka s hranou 5 cm se rozřízne na kostky, každá s hranou 1 cm. Najděte poměr celkového povrchu jedné z malých kostek k celkové ploše velké kostky. - Hemisférami 83937
Tobolka léku je válec se dvěma hemisférami přilepenými na každém konci. Jeho délka je 14 mm a jeho průměr je 5 mm. Najděte její povrch. - Najděte 84125
Povrch dvou koulí je v poměru 1:4. Najděte poměr jejich objemů.
Pokud jsou objem a povrch koule číselně stejné, najděte její poloměr.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
