Konjugát 83061
Tři vektory A, B a C souvisí takto: A/C = 2 při 120 stupních, A + B = -5 + j15, C = konjugát B. Najděte C.
Správná odpověď:
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také kalkulačku s komplexními čísly.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také kalkulačku s komplexními čísly.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- geometrie
- vektor
- algebra
- rovnice
- aritmetika
- násobení
- dělení
- sčítání
- planimetrie
- trojúhelník
- čísla
- komplexní čísla
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Komplexní 53641
Najděte čísla a a b, pokud (a - bi) (3 + 5i) je komplexní konjugát (-6 - 24i) - Jsou dány 2
Jsou dány vektory v=(2,7; -1,8), w=(-3;2,5). Určete souřadnice vektorů: a=v+w, b=v-w, c=w-v, d=2/3v - Kolmá a rovnoběžná
Potřebuji matematickou pomoc v tomto problému: jsou dány dva trojrozměrné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnoběžná s a a w je kolmá na a. Najděte souřadnice vektorů v a w. - Z=-√2-√2i 74744
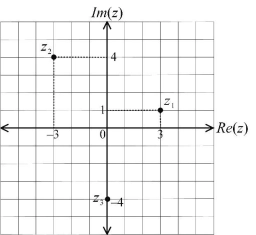
Nechť komplexní číslo z=-√2-√2i, kde i² = -1. Najděte |z|, arg(z), z* (kde * označuje komplexní konjugát) a (1/z). V případě potřeby napište své odpovědi ve tvaru a + i b, kde ai b jsou reálná čísla. Označte polohy čísel z, z* a (1/z) na Argandově diagram
- Úhel mezi vektory
Najděte úhel mezi danými vektory a zaokrouhlete výsledek na desetinu stupně. u = (-22, 11) a v = (16, 20) - Vektory - základní operace
Dáno jsou body A [-11; 14] B [-1; -18] C[10; -20] a D[19; 15] a. Určitě souřadnice vektorů u = AB v = CD s = DB b. Vypočítejte vektorový součet u + v c. Vypočítejte rozdíl vektorů u-v d. Určitě souřadnice vektoru w = -4.u - Vektory
Pro vektor w platí: w = +4v. UrčPro vektor w platí: w = +4v. Určete souřadnice vektoru w, jestliže u=(-4, 2), v=(0, 3) - Cukry
V jakém poměru musí být smíšeny dva druhy cukru, které stojí v hodnotě ; 390 a ; 315 na kg, aby se vyrobila směs v hodnotě ; 369 na kg? - Lichoběžník 5341
Lichoběžník, kde AB je rovnoběžná s CD, má úhel A : úhel D = 4 : 5, úhel B = 3x-15 a úhel C = 4x+20. Najděte úhel A, B, C a D.
- (a+8)/2-3(a+10)/5=1 82163
Vyřešte - najděte hodnotu neznámé a v rovnici (a+8)/2-3(a+10)/5=1. - Rovnici: 83085
Najděte neznámé číslo/smíšené číslo N v dané rovnici: N + 3 1/2 = 6 3/4 - (3x+1)/8+15 32541
Řešte následující rovnici se zlomky: (5x+1)/3+ (17-x)/2 = (3x+1)/8+15 - Eliminační metoda
Řešte soustavu lineárních rovnic eliminační metodou: 5/2x + 3/5y= 4/15 1/2x + 2/5y= 2/15 - Úhel
Daná je přímka p určena rovnicí y = (-8)/(6) x +78. Vypočítejte ve stupních velikost úhlu přímky p s osou y.
- Fahrenheita(F) 30501
Při převodu stupňů Celsia(C) na stupně Fahrenheita(F) se používá vztah: F = C . 9/5 + 32. Kolik stupňů Celsia mají ve městě New York, pokud jim teploměr ukazuje 23 stupňů Fahrenheita? - Abs a vektory
Jsou dány vektory a=(4,2), b=(-2,1). Vypočítejte: a) |a+b|, b) |a|+|b|, c) |a-b|, d) |a|-|b|. - Výpočty
Zlomky: 14/17 . 34/56 + 6/9 + 10/13 : 5/26 = 10/16 - ¼ + 15/18 : 5/9 = ¾ . (25/42 - 3/7) +16/21 : 4/7 = 2. Celá čísla: (-12) + (-6). (-2) - (-14) : 2 = 35 : (-5) + (-12) . 2 + (-6) = 42 : (-3) . (-5) - (-12)+ (-16) =
