Absolútna hodnota - príklady - strana 3 z 7
Pokyny: Vyriešte každú úlohu starostlivo a ukážte svoje celé riešenie. Ak je to vhodné, vykonajte skúšku správnosti riešenia.Počet nájdených príkladov: 128
- Dva vlaky 6
Dva vlaky opustili Londyn na ceste do Brightonu. Jeden o 14,00 a druhy o 14,20. Jeden vlak sa pohybuje rychlostou 120/km za hodinu. Druhy 150/km za hodinu. Ako daleko sa od seba budu nachadzat o tretej hodine? - Vzdialenosť
Vypočítajte vzdialenosť bodu A [0, 2] od priamky prechádzajúcej bodmi B [9, 5] a C [1, -1]. - Na priamke
Na priamke p: 3 x - 4 y - 3 = 0, stanovte súradnice bodu C, ktorý je rovnako vzdialený od bodov A [4, 4] a B [7, 1]. - V kružnici 2
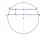V kružnici s priemerom 70 cm sú narysované dve rovnobežné tetivy tak, že stred kružnice leží medzi tetivami. Vypočítaj vzdialenosť týchto tetív, ak jedna z nich má dĺžku 42 cm a druhá 56 cm.
- Uhol telesových uhlopriečok
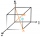Pomocou vektorového skalárneho súčinu (bodky) produktu vypočítajte uhol telesových uhlopriečok kocky. - Dĺžka úsečky
Predpokladajme, že viete, že dĺžka úsečky je 15, x2 = 6, y2 = 14 a x1 = -3. Nájdite možnú hodnotu y1. Existuje viac ako jedna možná odpoveď? Prečo áno alebo prečo nie? - Dve tetivy 4
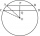V kružnici s r=26 cm sú narysované 2 rovnobežné tetivy . Jedna tetiva má dĺžku t1=48 cm a druhá má dĺžku t2=20cm, pričom stred leží medzi nimi. Vypočítaj vzdialenosť dvoch tetív. - Zvierajú 13551
Aký uhol zvierajú ručičky hodín: a/v 16 hodín 15minút b/v 8 hodín a 4 minúty - Abs v nerovnici
Rieš na Z - nerovnicu s absolútnou hodnotou: |x-18|+4 > 1
- Čo dostanem
Čo dostanem vynasobenim absolútnej hodnoty k číslu -0,7 a prevrateneho čísla k číslu 10 Čo dostanem vydelenim opačného čísla k číslu -14/8 a prevrateneho čísla k číslu 4 - MO Z7–I–3 2019
Roman má rád kúzla a matematiku. Naposledy čaroval s trojcifernými alebo štvorcifernými číslami takto: • z daného čísla vytvoril dve pomocné čísla tak, že ho rozdelil medzi ciframi na mieste stoviek a desiatok (napr. Z čísla 581 by dostal 5 a 81), • pomoc - Vzdialenosti 9221
Vo vetvách stromu sú dva leňochody. Jeden je vo vzdialenosti 2,5 m od kmeňa a druhý na druhej strane stromu vo vzdialenosti 4 m od kmeňa. Leňochi sa vydajú zoznámiť sa. Vypočítajte v akej vzdialenosti od kmeňa sa stretnú, pokiaľ lezú rovnakou konštantnou - Pozorovateľ 2
Pozorovateľ sleduje z vrchola kopca, ktorý je 75 m nad hladinou jazera, dve loďky v hĺbkových uhloch 64° a 48°. Určte vzdialenosť medzi loďkami, ak obe loďky a pozorovateľ sú v tej istej zvislej rovine. - Polohový 3
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase
- Polohový 2
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čas - Vektory 5 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t =
- Polohový vektor
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t = - Stan a maják
Marcel (bod J) leží v tráve a vidí v zákryte vrchol stanu (bod T) a za ním vrchol majáka (P). |TT'| = 1,2m, |PP'| = 36m, |JT'| = 5m. Marcel leží 15 m odbrehu mora (M). Vypočítajte vzdialenosť majáka od brehu mora – |P'M| . - Štvorec
Štvorec ABCD má stred S [-3, -2] a vrchol A [1, -3]. Určte súradnice ostatných vrcholov štvorca.
Na hodinovom číselníku zviera hodinová a minútová ručička uhol alfa. Ak viete že je 10 hodín a 12 minút potom veľkosť uhla je?Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
