Tangent - practice problems - page 4 of 15
Number of problems found: 292
- Deviation - slope angle
Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30° from the base plane. - Function x*tanx
Functions: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Find; i)vertical and horizontal asymptotes iii)the interval of decrease and increase iii)Local maxima and local minima iv)interval of concavity and inflection. And sketch the graph. - Building 67654
The 15 m high building is 30 m away from the river bank. The river's width can be seen from the roof of this building at an angle of 15 °. How wide is the river? - Horizontal 66434
The lower station of the cable car in Smokovec is at an altitude of 1025m, and the upper station at Hrebienk is at an altitude of 1272m. Calculate the climb of the cable car if the horizontal distance between the slopes is 1921m.
- Horizontal 64864
The meter stick is located on the meridian plane and deviated from the horizontal plane to the north by an angle of magnitude 70°. Calculate the length of the shadow cast by a meter stick at true noon if the Sun culminates at an angle of 41°03'. - Hypotenuse and center
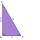Point S is the center of the hypotenuse AB of the right triangle ABC. Calculate the area of triangle ABC if the line on the hypotenuse is 0.2 dm long and if angle ∢ACS is 30°. - Right-angled trapezoid
A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is: - Observation 63194
Determine the height of the cloud above the lake's surface if we see it from place A at an elevation angle of 20° 57'. From the same place A, we see its image in the lake at a depth angle of 24° 12'. Observation point A is 115m above the lake level. - Cross-section 62964
The owner must cover the carport with a hipped roof with a rectangular cross-section of 8 m x 5 m. All roof surfaces have the same slope of 30°. Determine the price and weight of the roof if 1 m² cost €270 and weighs 43 kg.
- Perpendicular 62824
The magnetic induction vector at a given field location has the direction: a) to the south magnetic pole b) tangent to the induction line c) to the north magnetic pole d) perpendicular to the tangent to the induction line - The ladder
The ladder makes an angle of 2°30' with the wall and reaches a height of 2.3 m. How far is the ladder from the wall? - Raindrops
The car runs on a horizontal track at a constant speed of 20 m2-1. It is raining. Raindrops fall in a vertical direction at a speed of 6 m/s. a) How fast is the speed of the drops relative to the car windows? b) What is the angle of the raindro - Side wall planes
Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Sphere submerged in the cone
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
- The chimney
How high is the chimney if we see it from a distance of 60 m at an angle of 42°? - Regular octagon pad
You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Approximation of tangent fx
What is the nontrigonometric formula (not a polynomial fit) for the growth curve that solves algebraically for the increase between tan(1 degree) and tan(2 degrees) continuing up to the tangent(45 degrees)? Okay, to use pi Check calculation for 12°. - Trapezoids
In the isosceles trapezoid ABCD we know: AB||CD, |CD| = c = 8 cm, height h = 7 cm, |∠CAB| = 35°. Find the area of the trapezoid.
A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
