Square root + length - practice problems
Number of problems found: 372
- A tree 3
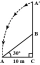A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. - Three inscribed objects
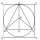A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square. - A chord 2
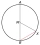A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle. - Two points
M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN.
- A boat 3
A boat takes 1 hour longer to go 36 km up a river than to return. If the river flows at 3 km/h, find the rate at which the boat travels in still water. - Missing side length
Use the Pythagorean Theorem (a² + b²=c²) to find a unknown side length: a = 5; c = 13 ; b=? - PQR - Euclid
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Smaller square
Let the points A, B, C and D are midpoints of the sides of the square PQRS. If the area of PQRS is 100 sq cm, what is the area of the smaller square ABCD? - The area 5
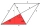The area of a rhombus is 144 sq cm. If one of the diagonals is double the other, find the length of the diagonals.
- An equilateral triangle 2
If the sides of an equilateral triangle are increased by 2 meters, the area is increased by 7√3 square meters. Find the length of the side. - A tree 2
A tree is broken at a height of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree. Find the original height of the tree. - Two chords 6
A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle. - An isosceles triangle
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - Cuboid - sum of edges length
Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
- A frustum
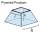A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - A lighthouse
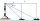A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - A right triangle A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
- Two chords 2 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
- Piece of a wire A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
Mrs. Clarke is teaching a 5th-grade class. She is standing 40 feet in front of Valeria. Sarah is sitting to Valeria's right. If Sarah and Mrs. Clarke are 50 feet apart, how far apart are Valeria and Sarah?Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
