Examples for secondary school students - page 196 of 222
Number of problems found: 4435
- Target
Peter, Martin, and Jirka were a fire in a particular target, with only three fields with values of 12, 18, and 30 points. All boys were firing with the same number of arrows, and all the arrows hit the target, and the results of every two boys differed by - Sphere and cone
Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone? - Triangular prism
The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism. - Hockey players
After we cycle, five hockey players sit down. What is the probability that the two best scorers of this crew will sit next to each other?
- Sinus
Determine the smallest integer p for which the equation 4 sin x = p has no solution. - Quadratic function
It is given a quadratic function y = -4x²+5x+c with an unknown coefficient c. Determine the smallest integer c for which the graph of f intersects the x-axis at two different points. - Cross-sections of a cone
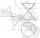Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Line
Straight-line passing through points A [-3; 22] and B [33; -2]. Determine the total number of points of the line in which both coordinates are positive integers. - Mystery of stereometrie
Two regular tetrahedrons have surfaces 76 cm² and 171 cm². In what ratio are their volumes? Write as a fraction and as a decimal rounded to 4 decimal places.
- Snowman 2
On the medal, which has the shape of a circle with a diameter 18 cm, is sketched a snowman so that the following requirements are met: 1. snowman is composed of three circles, 2. space over the snowman is the same as under it, 3. diameters of all circles - Mother and daughter
Three years ago, the mother was three times older than the daughter. After nine years, she will be only twice as old. How old is the mother (and daughter)? - Two workers
Two workers will do certain work for 12 days. After eight days of working, one was removed, and the other finished the job alone in 10 days. For how many days would you do this work alone for each worker? - The dice
What is the probability of events if we throw a dice rolled less than 1? - Pedestrian up-down hill
The pedestrian goes for a walk first on the plane at 4 km/h, then uphill at 3 km/h. Then it is in the middle of the route, turns back, and goes downhill at 6 km/h. The total walk was 6 hours. How many kilometers went pedestrians?
- Electrics - conductor
The wire is 107 meters long at 0 °C, and at every temperature increase of 1 °C, the length increases by 0.15 mm per 1 m length of wire. Determine a function that represents the wire's overall length as a temperature function. What is the length of the wir - Lottery
Fernando has two lottery tickets, each from the other lottery. In the first is 973 000 lottery tickets from them wins 687 000, the second has 1425 000 lottery tickets from them wins 1425 000 tickets. What is the probability that at least one Fernando's ti - UV radiation
The glass of 1 mm thickness absorbs 5.3% of UV radiation passing through. How many percent of UV rays absorb glass with a thickness of 2.3 cm, made from 1 mm thick those glasses? - Pool 2
The first supply is by the pool fill for five hours and the second fill for six hours. The drain should be drained for 15 hours. How many hours is the pool full when we open both inlets now, and the outlet opens two hours later? - Geometric sequence 4
It is given geometric sequence a3 = 7 and a12 = 3. Calculate s23 (= sum of the first 23 members of the sequence).
Paul put 10000 in the bank for 6 years. Calculate how much you will have in the bank if he does not pick earned interest or change deposit conditions. The annual interest rate is 3.5%, and the tax on interest is 10%.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
