Triangle - high school - practice problems
Number of problems found: 1036
- The angles 5
The angles of a triangle are in arithmetic progression (AP). The greatest angle is twice the least. Find all the angles. - The hypotenuse
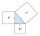The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides is 4 meters, find the other sides. - One side 3
One side of a triangular banner is 1 1/2 times longer than the second side and 2cm shorter than the third side. The perimeter of the triangle is 98cm. How long is the shortest side? - General right triangle
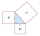In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
- EE school boarding
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - Prove 2 Prove that the minimum number of straight single cuts/strokes needs to divide a given right-angled triangle or an obtuse-angled triangle into a collection of all acute-angled triangles is seven(7).
- Cplx sixth power
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - The vertices
The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C. - The angles 6
If the angles of a triangle are in the ratio 2 : 3: 4. Find the value of each angle.
- A triangle 10
A triangle has vertices at (4, 5), (-3, 2), and (-2, 5). What are the coordinates of the vertices of the image after the translation (x, y) arrow-right (x + 3, y - 5)? - Height or altitude
Find the altitude (in cm) of side MT of triangle MNT with side MN = 36 cm, MT = 36 cm and NT = 48 cm. - The coordinates 4 The coordinates of the vertices of ∆ABC are respectively (-4, -2), (6, 2) and (4, 6). Find the centroid G of ∆ABC.
- A radio antenna
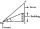Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Tower + pole
On the horizontal plane, there is a vertical tower with a flag pole on its top. At a point 9 m away from the foot if the tower, the angle of elevation of the top and bottom of the flag pole are 60°and 30° respectively. Find the height of the flag pole.
- A man 23
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - The coordinates 3
The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex? - Triangle 82
Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR? - Angle of elevation
From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th - The angle 9
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
