Examples for secondary school students - page 185 of 222
Number of problems found: 4435
- Buttercups 2031
Paul has eight dry mushrooms, 1/2 fewer oaks, and cossacks, five times more than buttercups. Cossacks and buttercups have a total of 3 times more than dry mushrooms. How many mushrooms do they have together? And how many buttercups and how many Cossacks? - Railway
The railway line climbs 8 permille between points A and B, whose horizontal distance is 1.5 km. It climbs 14 permille between points B and C, which have a horizontal distance of 900 m. Calculate the differences in altitudes between points A and C. - Rectangular triangles
The lengths of the corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and - Locomotive
Locomotive pulled a permanent train load of 200 kN horizontally along the track of 5km. What work has it done?
- Height difference
What height difference is overcome if we pass a road 1 km long with a pitch of 21 per mille? - Win in raffle
The raffle tickets were sold to 200, 5 of which were winning. What is the probability that Peter, who bought one ticket, will win? - Railway
The railway line had a 5.8 km segment climb nine permille. How many meters does the track ascent? - RT leg and perimeter
The right triangle ABC with hypotenuse c has the length of a leg a= 84 and the perimeter of the triangle o = 269. Calculate the size of the sides of the triangle ABC. - Chimney
The lower circumference of the chimney is 12.57 m, and the top circumference is 5.655 m. The slope of the walls is 87°. Find the height of the chimney.
- Coffee shop
The coffee shop brought two types of coffee total of 50 kg. The first type was CZK 220 per kilogram, and the second type was 300 CZK per 1 kg. All the coffee traders earned CZK 12,000. How many kilograms of coffee of the first type and how many kilograms - Water reservoir
The water reservoir is filled through one inlet 4 hours later than both, then another 9 hours later. For how long is each filled out separately? - The cone
The cone's lateral surface area is 4 cm², and the area of the base is 2 cm². Find the angle in degrees (deviation) of the cone sine and the cone base plane. (The cone side is the segment joining the vertex cone with any point of the base circle. All sides - Jar
The jar has the shape of a cylinder. Height of jar h = 8 cm, and jar diameter D is 8 cm. After rolling the pot, some water spilled, and the water level accurately reached half of the base. The water level makes a parabola with the same diameter. How to ca - Equilateral triangle v2
An equilateral triangle has a perimeter 36 dm. What is its area?
- Hexagonal pyramid
The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high. - Cube from sphere
What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm? - Height of the arc - formula
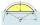Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this? - SD - mean
The mean is 10, and the standard deviation is 3.5. If the data set contains 40 data values, approximately how many of the data values will fall within the range of 6.5 to 13.5? - Prism
The volume of a tetrahedral prism is 2.43 m³. The prism's base is a parallelogram with a side of 2,5dm and height ha = 18cm. Calculate the height of the prism.
In the garden with an area of 8 ares, rain 40hl of water. To what heights leveled water?Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
