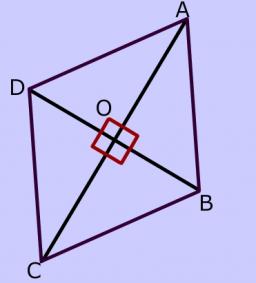
Diagonals in diamond
In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals.
Final Answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Calculate 263
Calculate the area of a rhombus whose diagonals are u = 12 and v = 19. - Rhombus diagonals
In the rhombus ABCD, the sizes of the diagonals e = 24 cm and f = 10 cm are given. Calculate the side length of the diamond and the size of the angles, and then calculate the area of the diamond. - Diagonals in diamons/rhombus
Rhombus ABCD has a side length AB = 4 cm and a length of one diagonal of 6.4 cm. Calculate the length of the other diagonal. - Rhombus and diagonals
The lengths of the diamond diagonals are e = 48 cm f = 20 cm. Calculate the length of its sides. - Diamond
Calculate the length of the two diagonals of the diamond if: a = 13 cm v = 12 cm - Rhombus - diagonals
Rhombus ABCD has diagonals u₁ and u₂ that make an angle of 60° with each other. Side a = 80 cm and side b = 50 cm. Calculate the area of the rhombus. - Diamond ABCD
In the diamond ABCD, the diagonal e = 24 cm, and the size of angle SAB is 28 degrees, where S is the intersection of the diagonals. Calculate the circumference of the diamond.
