Velocity ratio
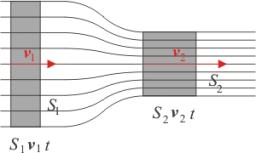
Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the fluid velocity [v] the same.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
Tip: Our volume units converter will help you convert volume units.
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
Tip: Our volume units converter will help you convert volume units.
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rectangular 2885
A total of ten exhibitors gathered at the long-haired cat show. It was exhibited in a rectangular room with two rows of tables, as shown. The cats were marked with different numbers from 1 to 10, and one cat sat on each table. Determine which cat was rate - Rubberized 19963
The circular pool with a diameter of 3.5 m is covered with a circular tarpaulin made of rubberized fabric for CZK 110 per square meter. Determine how much the tarpaulin cost if you know that its radius is 25 cm larger than the radius of the pool. - MIT 1869
You know the length of parts 9 and 16 of the hypotenuse, at which a right triangle's hypotenuse is divided by a height. The task is to find the lengths of the sides of the triangle and the length of line x. This assignment was part of the Massachusetts In - Circumference 82489
An isosceles trapezoid has one base twice as short as the other. Its area is 42 cm², and its height is 4 cm. Calculate its circumference if you know that the arm is 5.3 cm long.
- Calculate 83261
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 - A Cartesian framework
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Perpendicular projection
Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0.
