Příklady na zlomky - strana 112 z 126
Zlomek je matematický výraz, který představuje část celku. Píše se jako dvě čísla oddělená čarou nebo lomítkem (zlomkovou čarou), přičemž číslo nahoře se nazývá čtenář a číslo v dolní části se nazývá jmenovatel. Čtenář představuje počet částí celku, které se zvažují, a jmenovatel představuje celkový počet částí, na které je celek rozdělen. Například, pokud máte pizzu a chcete ji sdílet se 3 lidmi, každý obdrží 1/3 pizzy. Čtenář (1) představuje počet částí, které obdrží každá osoba, a jmenovatel (3) představuje celkový počet částí, na které je pizza rozdělena. Zlomky lze zjednodušit, porovnávat, sčítat, odečítat, násobit a dělit stejně jako jakákoli jiná čísla.Počet nalezených příkladů: 2517
- Na mapě 7
Určete měřítko mapy, je-li les tvaru trojúhelníku o rozměrech 1,6 km, 2,4 km a 2,7 km na mapě zakreslen jako trojúhelník o stranách délek 32 mm, 48 mm a 54 mm. - Koeficient 81094
Automobil se pohybuje po vodorovné cestě rychlostí 15m/s. Po vypnutí motoru automobil projel ještě dráhu 225m. Jaký byl koeficient tření při tomto pohybu? - Vystoupilo 69094
Letadlo o hmotnosti 61 t vystoupilo z výšky 1000 m do výšky 3000 m, přičemž zvětšilo rychlost ze 170 m/s na 210 m/s. Jakou práci vykonali motory letadla? - Předpokladu 80572
Projektil o hmotnosti 20 g vystřelí rychlostí 800m. s -1 se zaryje 100 mm hluboko do muriva. Jak dlouho ve zdivu brzdí za předpokladu rovnoměrně zpomaleného pohybu.
- Západ-jih
Pozoroval stojící západně od věže vidí její vrchol pod výškovým úhlem 45 stupňů. Poté, co se posune o 50 metrů na jih, vidí její vrchol pod výškovým úhlem 30 stupňů. Jak vysoká je věž? - Rovnostranného 81142
Rotační těleso vzniklo rotací rovnostranného trojúhelníku o délce strany a=2 cm kolem jedné z jeho stran. Vypočítejte objem tohoto rotačního tělesa. - Vypočítej 70744
Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°. - Trojúhelníku 70824
Jedna odvěsna pravoúhlého trojúhelníku ABC má délku a= 14 cm a poloměr kružnice vepsané do tohoto trojúhelníku r= 5 cm. Vypočítejte délku přepony a jeho druhé odvěsny. - Určete 20
Určete velikost úhlu mezi vektory u =(3; -5) a v = (10;6)
- Střecha 11
Střecha má tvar pláště pravidelného šestibokého jehlanu o stěnové výšce v= 5 m a podstavné hraně a= 4 m. Vypočtěte spotřebu plechu na pokrytí střechy, počítáme-li s 15 % ztrát. - Nad odvěsnami
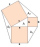Nad odvěsnami a přeponou jsou sestrojeny čtverce. Spojením vnějších vrcholů sousedních čtverců vzniknou tři trojúhelníky. Dokaž, že jejich obsahy jsou stejné. - 4b jehlan 4
Vypočítejte povrch pravidelného čtyřbokého jehlanu, je-li dáno: a= 3,2 cm v= 19 cm Postup: 1) výpočet výšky boční stěny 2) obsah podstavy 3) obsah pláště 4) povrch pravidelného čtyřbokého jehlanu - Stěnové úhlopříčky
Pokud jsou stěnové úhlopříčky kvádru x, y a z (diagonály), pak najděte objem kvádru. Vyřešte pro x = 1,2, y = 1,8, z = 1,4 - Čtverečních 74024
Úhlopříčka osového řezu rotačního válce je 6 cm a jeho povrch je 30cm čtverečních. Vypočítej poloměr podstavy.
- Rovnoběžníku 65954
V rovnoběžníku ABCD platí AB = 8, BC = 5, BD = 7 . Vypočtěte velikost úhlu α = ∠DAB (ve stupních). - Pravidelného 71484
Střecha věže má tvar pravidelného 4-bokého jehlanu a výškou 4m a hranou podstavy 6m. Zjistilo se, že je poškozeno 25% krytiny na střeše. Kolik metrů čtverečních krytiny je potřeba k opravě střechy? - Bazén 22
Bazén o délce l = 50 m a šířce s = 15 m má u stěny v nejmělčí části hloubku h1 = 1,2 m. Hloubka se pak plynule zvětšuje do hloubky h2 = 1,5 m uprostřed bazénu a dál se opět plynule zvětšuje do hloubky h3 = 4,5 m u stěny v nejhlubší části bazénu. Uvažujte - Sklon úsečky
Úsečka má své koncové body na souřadnicových osách a formuje s nimi trojúhelník s plochou 36 čtverečních jednotek. Úsečka prochází bodem (5,2). Jaký je sklon úsečky? - Pravidelného 7833
Věž má tvar pravidelného čtyřbokého jehlanu s podstavou hranou 0,8m. Výška věže je 1,2 metru. Kolik metrů čtverečních plechu je třeba na pokrytí počítáme-li osm procent na spoje a překrytí?
Dřevená deska dlouhá 2,5m má pruřez tvaru pravidelného lichobežníku jehož rovnobežné strany májí delku 1,2dm a 8cm vyška lichobežníka je 3cm. Vypočtete: a) povrch desky pro vypočet spotřeby mořidla b) hmotnost desky je-li hustota dřeva je 600kg/m³ c) koliMáš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
