Geometrie - slovní úlohy a příklady - strana 29 z 37
Počet nalezených příkladů: 726
- Rozdělit řezem
Daný je kužel s poloměrem podstavy 10 cm a výšce 12 cm. V jaké výšce nad podstavou ho máme rozdělit řezem rovnoběžným s podstavou, aby objemy obou vzniklých teles byly stejné? Výsledek uveďte v cm. - Přímky
Kolika přímkami lze spojit 8 bodů, pokud tři body leží na jedné přímé a z ostatních žádné tři neleží na téže přímce? - Vzdálenost bodů 2
Vypočítej vzdálenost bodů X[1,3] od středu úsečky x=2-6t, y=1-4t; t je z intervalu <0,1>. - Učitel 2
Učitel má k dispozici 12 příkladů z geometrie a 15 příkladů z aritmetiky. Kolik písemek může vytvořit, jestliže v písemce chce mít 3 příklady z geometrie a 5 z aritmetiky?
- Přeřízneme jehlan
Pravidelný čtyřboký jehlan má výšku 40 cm a stranu podstavy 21 cm. Jehlan přeřízneme v poloviční výšce. Jak velký objem budou mít obě části? - Střed úsečky
Délka úseček MG = 7x-15 a FG = 33 Bod M je střed FG. Najdi neznámou x. - Střední příčka
Střední příčka lichoběžníka p je 18,6 cm a základna a=29,8 cm. Vypočítejte velikost druhé základny c. - Souřadnice průsečíku
V pravoúhlé soustavě souřadnic je narýsován obdélník ABCD. Vrcholy obdélníku jsou určeny těmito souřadnicemi A= (2,2) B= (8,2) C= (8,6) D= (2,6) Určete souřadnice průsečíku úhlopříček obdélníku ABCD - Body v rovině
V rovině je dáno 12 bodů, z nichž 5 leží na jedné přímce. Kolik různých přímek určují dané body?
- Súradnice trojuholníka
Trojúhelník je dán třemi vrcholy: A [0,0] B [-4,2] C [-6,0] Vypočítejte V (průsečík výšek), T (těžiště), O - střed kružnice opsané - Velký kužel
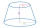Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl? - Roviny
Daných je n bodů, z nichž žádné tři neleží na jedné přímce a žádné čtyři neleží v jedné rovině. Kolik rovin lze vést těmito body? Kolik je rovin, pokud jich je pětinásobně více než daných bodů? - Prostoru 3570
V prostoru je 12 bodů, přičemž žádné 3 neleží na přímce. Kolik různých rovin je určeno těmito body? - Pětiúhelník
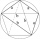Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA
- Průsečík přímky a roviny
Je dán pravidelný čtyřboký jehlan ABCDV, uvnitř jeho hrany AV je bod M, na prosloužené úsečce DC za bod C je bod N. Sestrojte průsečnici roviny MNV s rovinou BCV a průsečík přímky MN a roviny BCV. - Obdélník
V obdélníku se stranami 3 a 9 vyznačíme úhlopříčku. Jaká je pravděpodobnost, že náhodně zvolený bod uvnitř obdélníku je blíže k této úhlopříčce, jako k libovolné straně obdélníku? - Menealovy 26771
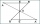Ukažte (pomocí Menealovy věty), že těžiště dělí těžnici v poměru 1:2. - Rovnostranny kužel
Do nádoby tvaru rovnostranného kužele, jehož podstava má poloměr r = 6 cm nalijeme tolik vody, že se naplní jedna třetina objemu kužele. Do jaké výšky bude sahat voda, pokud kužel obrátíme dnem vzhůru? - Tajný poklad
Skauti mají stan ve tvaru pravidelného čtyřbokého jehlanu se stranou podstavy 4 m a výšce 3 m. Do stanu potřebují schovat válcovou nádobu s tajným pokladem. Určete poloměr r (a výšku h) nádoby tak, aby mohli schovat co nejobjemnější poklad.
Na rovné planině jsou kolmo vzhůru vztyčeny 2 sloupy. Jeden je vysoký 7 m a druhý 4 m. Mezi vrcholem jednoho sloupu a patou druhého sloupu jsou natažena lanka. V jaké výšce se budou lanka křížit? Předpokládejme, že se lanka neprověšují.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
