Unit conversion practice problems - page 95 of 120
The International System of Units (SI) is the standard system of units used in most countries around the world. It is based on seven base units: the meter for length, the kilogram for mass, the second for time, the ampere for electric current, the kelvin for temperature, the mole for amount of substance, and the candela for luminous intensity. These units can be converted to other units using conversion factors, such as the relationship between meters and centimeters (1 meter = 100 centimeters). Other common SI unit conversions include:1 liter = 1000 milliliters
1 gram = 1000 milligrams
1 joule = 1 watt-second
1 newton = 1 kilogram-meter per second squared
In the SI system, units can be multiplied or divided by powers of ten to create larger or smaller units. These multiples are called prefixes. The most common prefixes and their meanings are:
mega- (M) = 1,000,000 (e.g. 1 megahertz = 1,000,000 hertz)
kilo- (k) = 1000 (e.g. 1 kilogram = 1000 grams)
centi- (c) = 0.01 (e.g. 1 centimeter = 0.01 meters)
milli- (m) = 0.001 (e.g. 1 milliliter = 0.001 liters)
micro- (µ) = 0.000001 (e.g. 1 microgram = 0.000001 grams)
nano- (n) = 0.000000001 (e.g. 1 nanosecond = 0.000000001 seconds)
It is important to note that, when using these prefixes, the prefix should be written before the unit symbol.
Number of problems found: 2389
- Radiators
 Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1
Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1 - Calculate 6185
 Calculate the rectangle area measuring 0.9 m and 6 dm in cm square.
Calculate the rectangle area measuring 0.9 m and 6 dm in cm square. - Raindrops
 The train is moving at a speed of 60 km/h. Raindrops falling vertically in the absence of wind (with uniform movement due to the action of air resistance) leave traces on the windows of the train, deviating from the vertical direction by 30°. How fast are
The train is moving at a speed of 60 km/h. Raindrops falling vertically in the absence of wind (with uniform movement due to the action of air resistance) leave traces on the windows of the train, deviating from the vertical direction by 30°. How fast are - Spruce wood
 Calculate the weight of an edge made of spruce wood 6m long when the cross-section of the edge is 146cm square and if the density of the wood is 0.55 grams/cm cubic.
Calculate the weight of an edge made of spruce wood 6m long when the cross-section of the edge is 146cm square and if the density of the wood is 0.55 grams/cm cubic.
- Prism
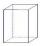 Calculate the height of the prism having a surface area of 448.88 dm² wherein the base is square with a side of 6.2 dm. What will be its volume in hectoliters?
Calculate the height of the prism having a surface area of 448.88 dm² wherein the base is square with a side of 6.2 dm. What will be its volume in hectoliters? - Rainfall
 The annual average rainfall in India was 26 461 mm in Cherrapunji in 1981. How many hectoliters of water fell on one square meter? Would you fit this amount of water into a cube of three meters?
The annual average rainfall in India was 26 461 mm in Cherrapunji in 1981. How many hectoliters of water fell on one square meter? Would you fit this amount of water into a cube of three meters? - Diameter 81760
 Winding drum length 180mm, initial diameter 60mm. Using a 6mm rope with a length of 50m, what will be the diameter of the wound drum with the rope?
Winding drum length 180mm, initial diameter 60mm. Using a 6mm rope with a length of 50m, what will be the diameter of the wound drum with the rope? - Runcated pyramid teapot
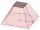 The 35 cm high teapot has the shape of a truncated pyramid with the length of the edge of the lower square base a=50 cm and the edges of the rectangular base b: 20 cm and c: 30 cm. How many liters of water will fit in the teapot?
The 35 cm high teapot has the shape of a truncated pyramid with the length of the edge of the lower square base a=50 cm and the edges of the rectangular base b: 20 cm and c: 30 cm. How many liters of water will fit in the teapot? - Calculate 3016
 Calculate the height of the cylinder based on its surface S and the radius of the base r. a) r = 2 cm, S = 120 cm square b) r = 7 dm, S = 4,000 dm square c) r = 0.2 m, S = 20 square meters
Calculate the height of the cylinder based on its surface S and the radius of the base r. a) r = 2 cm, S = 120 cm square b) r = 7 dm, S = 4,000 dm square c) r = 0.2 m, S = 20 square meters
- Diamond
 The diamond has a circumference of 48cm. Calculate the length of its side in dm.
The diamond has a circumference of 48cm. Calculate the length of its side in dm. - Observatory and aircraft
 The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee
The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee - Triangular 8227
 The teacher cast the gold in the shape of a regular triangular pyramid with a base edge length of 12 cm and a height of 8 cm. The density of gold is 19,320 kg/m³. What is the weight of the casting?
The teacher cast the gold in the shape of a regular triangular pyramid with a base edge length of 12 cm and a height of 8 cm. The density of gold is 19,320 kg/m³. What is the weight of the casting? - Gutter pipe
 How many m² of sheet metal is required to produce a 12 m long and 18 cm wide gutter if a 7% bend is required?
How many m² of sheet metal is required to produce a 12 m long and 18 cm wide gutter if a 7% bend is required? - Truncated pyramid
 How many cubic meters is the volume of a regular four-sided truncated pyramid with edges of one meter and 60 cm and a high of 250 mm?
How many cubic meters is the volume of a regular four-sided truncated pyramid with edges of one meter and 60 cm and a high of 250 mm?
- Sphere slices
 Calculate the volume and surface of a sphere if the radii of a parallel cut r1=32 cm, r2=47 cm, and its distance v=21 cm.
Calculate the volume and surface of a sphere if the radii of a parallel cut r1=32 cm, r2=47 cm, and its distance v=21 cm. - Distance 6466
 The water tank is cuboid with a square base (the edge of the base is 3.2 m long) and 3 m high. It holds 25,600 liters of water. What is the distance of the water level from the upper base?
The water tank is cuboid with a square base (the edge of the base is 3.2 m long) and 3 m high. It holds 25,600 liters of water. What is the distance of the water level from the upper base? - Trunk
 Calculate the length of the biggest fishing rod that can be inserted into the trunk of a car with dimensions 152 x 82 × 81 cm.
Calculate the length of the biggest fishing rod that can be inserted into the trunk of a car with dimensions 152 x 82 × 81 cm. - The tank
 The tank is full up to 4/5 of the total height and contains 240 hl of water. The area of the base is 6 square meters. What is the height of the tank?
The tank is full up to 4/5 of the total height and contains 240 hl of water. The area of the base is 6 square meters. What is the height of the tank? - The pot
 The pot is in 1/3 filled with water. The bottom of the pot has an area of 329 cm². How many centimeters rise in water level in the pot after adding 1.2 liters of water?
The pot is in 1/3 filled with water. The bottom of the pot has an area of 329 cm². How many centimeters rise in water level in the pot after adding 1.2 liters of water?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
