The inscribed angle theorem of circle problems
Number of problems found: 40
- Angle over circle
In the figure, O is the center of the circle and AB is tangent at B. If angle OAB is 28 degrees find angle AOB. Figure is not scaled. - Subtended 83194
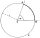A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Corresponding 82704
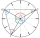On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles. - Quadrilateral 82395
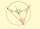The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral?
- Circumscribed 81759
In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle. - Calculate 71744
The triangle that connects on the dial: a) 2,7,9 b) 3,6,10 Calculate the size of the interior angles. - Three
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - Quadrilateral in circle
A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles. - Construction 55311
Construct a KLM triangle where side k is 6.7 cm, the line to the k side is 4.1 cm, and the LKM angle is 63 degrees. Write the construction procedure.
- Length of the chord
Calculate the length of the chord in a circle with a radius of 25 cm and a central angle of 26°. - The amphitheater
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle? - Angles - clock hands
Find the angle that the large hand makes with the small hand of the clock - the central angle at 12:30. Find the magnitude of the smaller angle (if possible). (Help: it's enough if you calculate how big an angle the hands make if they are 1 minute apart. - Dodecagon
Calculate the size of the smaller angles determined by lines A1 A4 and A2 A10 in the regular dodecagon A1A2A3. .. A12. Express the result in degrees. - Interior angles
In a quadrilateral ABCD, whose vertices lie on some circle, the angle at vertex A is 58 degrees, and the angle at vertex B is 134 degrees. Calculate the sizes of the remaining interior angles.
- Determine 19953
The distance between the tip of the minute hand and the center of the dial is 12 mm. Determine the distance traveled by the tip in 45 min. (draw a clock face and a minute hand and realize the distance it will cover in 45 min.) - Hexagonal pyramid
Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. - Quadrilateral 8405
Calculate the magnitude of the largest inner angle and the deviation of the diagonals in the quadrilateral, whose vertices correspond to points 1, 5, 8, and 12 on the dial. - Isosceles 7566
A right isosceles triangle is inscribed in the circle with r = 8 cm. Find triangle area S. How much percent does the triangle occupy the area of the circle? - Hexagon in circle
Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle.
In a rectangular triangle with sides lengths> a = 30cm and b = 12.5cm, the right angle is at vertex C. Calculate the radius of the inscribed circle.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
