Geometry - math word problems - page 10 of 157
Number of problems found: 3135
- Segments
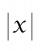Which of the pairs of numbers on the number line encloses the longest segment: ... - Find quadrant
Point Y is located at (4, -2) on a graph. Point Z is located five units to the left of Point Y. In which quadrant is Point Z located? - Points collinear
Show that the point A(-1,3), B(3,2), C(11,0) are col-linear. - Vector
Determine coordinates of the vector u=CD if C[12;-8], D[6,20].
- The modulus
Find the modulus of the complex number 2 + 5i - Scalar product
Calculate the scalar product of two vectors: (2.5) (-1, -4) - Vector - basic operations
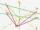There are given points A [-9; -2] B [2; 16] C [16; -2] and D [12; 18] a. Determine the coordinates of the vectors u=AB v=CD s=DB b. Calculate the sum of the vectors u + v c. Calculate the difference of vectors u-v d. Determine the coordinates of the vecto - Lengths 69314
We must cut three steel bars with 24 dm, 3 m, and 160 cm lengths into equal lengths. Find their maximum length and number. - MIT 1869
You know the length of parts 9 and 16 of the hypotenuse, at which a right triangle's hypotenuse is divided by a height. The task is to find the lengths of the sides of the triangle and the length of line x. This assignment was part of the Massachusetts In
- Individual 6270
Divide three lines with lengths of 12 cm, 24 cm, and 64 cm into equally long and, at the same time, the most extended possible parts. How long will the individual parts be, and how many will there be? - Dividing
Divide the three-line segments 13 cm, 26 cm, and 19.5 cm long for parts so that the individual pieces are equally long and longest. How long will the individual parts take, and how many will there be? - Saving in January
On the 1st of January, a student puts $10 in a box. On the 2nd, she puts $20 in the box, and so on, putting the same number of 10-dollars notes as the day of the month. How much money will be in the box if she keeps doing this for a) the first ten days of - A rope
Paul can cut a rope into equal lengths with no rope left over. The lengths can be 15cm, 18cm, or 25cm. What is the shortest possible length of the rope? - Four-sevenths 34451
In how many parts do I have to divide the line whose endpoints are the images of the numbers 0 and 1 on the number axis so that they can be displayed: three-fifths, four-sevenths, five-eighths, and six-sixths
- Jogging program
After knee surgery, the trainer tells the man to slowly return to his jogging program. He suggests a jogging program for 12 minutes each day for the first week. After that, he suggests increasing the time by 6 minutes per week. Find the number of minutes - Angles - clock hands
Find the angle that the large hand makes with the small hand of the clock - the central angle at 12:30. Find the magnitude of the smaller angle (if possible). (Help: it's enough if you calculate how big an angle the hands make if they are 1 minute apart. - Intersection 81611
Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides. - Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Mirror
How far must Paul place a mirror to see the top of the tower 12 m high? The height of Paul's eyes above the horizontal plane is 160 cm, and Paul is from the tower distance of 20 m.
Calculate the perimeter of triangle ABC if you know that it is similar to triangle EFG in which e=144 mm, f=164 mm, g=92 mm, and the similarity ratio is 4. Express the result in cm.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
