Intersection 81611

Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides.

Correct answer:

x₁ = -0.4545
y₁ = 2.9091
x₂ = -1.2727
y₂ = -2.4545

Step-by-step explanation:

A = (- 1, 3) B = (2, - 2) C = (- 4, - 3) m_{1} = \frac{B _{y} - A _{y}}{B _{x} - A _{x}} = \frac{( - 2 ) - 3}{2 - ( - 1 )} = - \frac{5}{3} = - 1 \frac{2}{3} ≐ - 1.6667 m_{2} = \frac{B _{y} - C _{y}}{B _{x} - C _{x}} = \frac{( - 2 ) - ( - 3 )}{2 - ( - 4 )} = \frac{1}{6} ≐ 0.1667 m_{3} = \frac{A _{y} - C _{y}}{A _{x} - C _{x}} = \frac{3 - ( - 3 )}{( - 1 ) - ( - 4 )} = 2 A B ⊥ h_{1} M_{1} = - 1 / m_{1} = - 1 / (- 1.6667) = \frac{3}{5} = 0.6 M_{2} = - 1 / m_{2} = - 1 / 0.1667 = - 6 M_{3} = - 1 / m_{3} = - 1 / 2 = - \frac{1}{2} = - 0.5 h_{1} : (x_{1} - C_{x}) = M_{1} \cdot (y_{1} - C_{y}) (x_{1} - A_{x}) = M_{2} \cdot (y_{1} - A_{y}) (x_{1} - (- 4)) = 0.59999999999999 \cdot (y_{1} - (- 3)) (x_{1} - (- 1)) = (- 5.9999999999999) \cdot (y_{1} - 3) x_{1} - 0.6 y_{1} = - 2.2 x_{1} + 6 y_{1} = 17 R o w 2 - R o w 1 \to R o w 2 x_{1} - 0.6 y_{1} = - 2.2 6.6 y_{1} = 19.2 y_{1} = \frac{1 9 . 2}{6 . 6} = 2.90909091 x_{1} = - 2.2 + 0.59999999999999 y_{1} = - 2.2 + 0.6 \cdot 2.90909091 = - 0.45454545 = - 0.4545 x_{1} = \frac{- 5}{1 1} ≐ - 0.454545 y_{1} = \frac{3 2}{1 1} ≐ 2.909091 Verifying Solution: T_{3} = \frac{x _{1} - B _{x}}{y _{1} - B _{y}} = \frac{( - 0 . 4 5 4 5 ) - 2}{2 . 9 0 9 1 - ( - 2 )} = - \frac{1}{2} = - 0.5 T_{3} = M_{3}

y_{1} = = 2.9091

s_{1} = \frac{A _{x} + B _{x}}{2} = \frac{( - 1 ) + 2}{2} = \frac{1}{2} = 0.5 s_{2} = \frac{A _{y} + B _{y}}{2} = \frac{3 + ( - 2 )}{2} = \frac{1}{2} = 0.5 s_{3} = \frac{B _{x} + C _{x}}{2} = \frac{2 + ( - 4 )}{2} = - 1 s_{4} = \frac{B _{y} + C _{y}}{2} = \frac{( - 2 ) + ( - 3 )}{2} = - \frac{5}{2} = - 2 \frac{1}{2} = - 2.5 s_{5} = \frac{A _{x} + C _{x}}{2} = \frac{( - 1 ) + ( - 4 )}{2} = - \frac{5}{2} = - 2 \frac{1}{2} = - 2.5 s_{6} = \frac{A _{y} + C _{y}}{2} = \frac{3 + ( - 3 )}{2} = 0 (x_{2} - s_{1}) = M_{1} \cdot (y_{2} - s_{2}) (x_{2} - s_{3}) = M_{2} \cdot (y_{2} - s_{4}) (x_{2} - 0.5) = 0.59999999999999 \cdot (y_{2} - 0.5) (x_{2} - (- 1)) = (- 5.9999999999999) \cdot (y_{2} - (- 2.5)) x_{2} - 0.6 y_{2} = 0.2 x_{2} + 6 y_{2} = - 16 P i v o t : R o w 1 \leftrightarrow R o w 2 x_{2} + 6 y_{2} = - 16 x_{2} - 0.6 y_{2} = 0.2 R o w 2 - \frac{1}{1} \cdot R o w 1 \to R o w 2 x_{2} + 6 y_{2} = - 16 - 6.6 y_{2} = 16.2 y_{2} = \frac{1 6 . 2}{- 6 . 6} = - 2.45454545 x_{2} = \frac{- 1 6 - 5 . 9 9 9 9 9 9 9 9 9 9 9 9 9 y _{2}}{1} = \frac{- 1 6 - 6 \cdot ( - 2 . 4 5 4 5 4 5 4 5 )}{1} = - 1.27272727 = - 1.2727 x_{2} = \frac{- 1 4}{1 1} ≐ - 1.272727 y_{2} = \frac{- 2 7}{1 1} ≐ - 2.454545 Verifying Solution: S_{3} = \frac{x _{2} - s _{5}}{y _{2} - s _{6}} = \frac{( - 1 . 2 7 2 7 ) - ( - 2 . 5 )}{( - 2 . 4 5 4 5 ) - 0} = - \frac{1}{2} = - 0.5 S_{3} = M_{3}

Did you find an error or inaccuracy? Feel free to write us. Thank you!

Showing 1 comment:

Dr. Math

To solve the problem, we need to find two specific points in triangle ABC with vertices at A(-1, 3) , B(2, -2) , and C(-4, -3) :

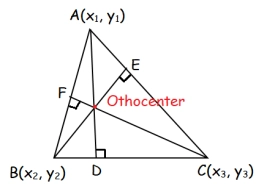
1. Orthocenter (Intersection of the Heights):

The orthocenter is the point where the three altitudes of the triangle intersect. An altitude is a perpendicular line from a vertex to the opposite side.

- Step 1: Find the slope of side BC :

Slope of BC = -3 - (-2)/-4 - 2 = -1/-6 = 1/6

The slope of the altitude from A to BC is the negative reciprocal:

Slope of altitude from A = -6

The equation of the altitude from A is:

y - 3 = -6(x + 1) ⇒ y = -6x - 3

- Step 2: Find the slope of side AC :

Slope of AC = -3 - 3/-4 - (-1) = -6/-3 = 2

The slope of the altitude from B to AC is the negative reciprocal:

Slope of altitude from B = -1/2

The equation of the altitude from B is:

y + 2 = -1/2(x - 2) ⇒ y = -1/2x - 1

- Step 3: Find the intersection of the two altitudes:

-6x - 3 = -1/2x - 1 ⇒ -12x - 6 = -x - 2 ⇒ -11x = 4 ⇒ x = -4/11

Substituting back:

y = -6(-4/11) - 3 = 24/11 - 33/11 = -9/11

So, the orthocenter is at:

(-4/11, -9/11)

2. Circumcenter (Intersection of the Perpendicular Bisectors of the Sides):

The circumcenter is the point where the perpendicular bisectors of the sides of the triangle intersect. It is the center of the circumcircle (the circle passing through all three vertices).

- Step 1: Find the midpoint of side AB :

Midpoint of AB = (-1 + 2/2, 3 + (-2)/2) = (1/2, 1/2)

The slope of AB is:

Slope of AB = -2 - 3/2 - (-1) = -5/3

The slope of the perpendicular bisector of AB is the negative reciprocal:

Slope of perpendicular bisector of AB = 3/5

The equation of the perpendicular bisector of AB is:

y - 1/2 = 3/5(x - 1/2) ⇒ y = 3/5x + 1/5

- Step 2: Find the midpoint of side BC :

Midpoint of BC = (2 + (-4)/2, -2 + (-3)/2) = (-1, -2.5)

The slope of BC is:

Slope of BC = 1/6

The slope of the perpendicular bisector of BC is the negative reciprocal:

Slope of perpendicular bisector of BC = -6

The equation of the perpendicular bisector of BC is:

y + 2.5 = -6(x + 1) ⇒ y = -6x - 8.5

- Step 3: Find the intersection of the two perpendicular bisectors:

3/5x + 1/5 = -6x - 8.5 ⇒ 3x + 1 = -30x - 42.5 ⇒ 33x = -43.5 ⇒ x = -43.5/33 = -29/22

Substituting back:

y = 3/5(-29/22) + 1/5 = -87/110 + 22/110 = -65/110 = -13/22

So, the circumcenter is at:

(-29/22, -13/22)

Final Answers:
- Orthocenter: (-4/11, -9/11)
- Circumcenter: (-29/22, -13/22)

yesterday Like

Tips for related online calculators

The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our trigonometric triangle calculator.