Cosine - practice problems - page 7 of 14
Number of problems found: 280
- Magnitude 25411
There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - Viewing angle
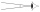The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure? - Pentagonal prism
The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism. - Triangle from median
Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5.
- Difference 23481
The distance as the crow flies between Dolní and Horní Ves is 3 km, and the steady climb is 5%. What is the height difference between Horní and Dolní Ves rounded to the nearest meter? - The bases
The bases of the isosceles trapezoid ABCD have 10 cm and 6 cm lengths. Its arms form an angle α = 50˚ with a longer base. Calculate the circumference and area of the ABCD trapezoid. - The rescue helicopter
The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site? - goniometric functions
Based on the fact that you know the values of sin and cos of a given angle and you know that tan (tangent) is their ratio, determine d) tan 120 ° e) tan 330 ° - The angle of view
Determine the angle of view at which the observer sees a rod 16 m long when it is 18 m from one end and 27 m from the other.
- Two groves
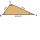Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'? - Decide 2
Decide whether points A[-2, -5], B[4, 3], and C[16, -1] lie on the same line - Trapezoid: 18703
In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Angle of the body diagonals
Using the vector dot product calculate the angle of the body diagonals of the cube. - Observation 17433
The aircraft flying just above point A can be seen from observation B, 2,400 meters away from point A, at an altitude of 52°30'. How high does the plane fly?
- Perpendicular line
According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was 3 km away from the starting point. They already deviated from the correct direction by 5° at the start. How far from the ta - Big Earth
What percentage of the Earth's surface is seen by an astronaut from a height of h = 350 km? Take the Earth as a sphere with a radius R = 6370 km. - 8-meter-long 16503
The 8-meter-long ladder is attached to the wall at an angle of 22 °. How high does it reach? - Power line pole From point A, the power pole is visible at an angle of 18 degrees. From place B, which we reach if we go from place A 30m towards the pillar at an angle of 10 degrees. Find the height of the power pole.
- Steps
Find the height between the two floors if you know that the number of steps between the two floors is 18, the gradient is 30º, and the step length is 28.6 cm. Report the result in centimeters to the nearest centimeter.
The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is considereDo you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
