Circle practice problems - page 41 of 49
Number of problems found: 972
- Calculate 80636
Calculate the distance of a chord 19 cm long from the center of a circle with a diameter of 28 cm. - Hexagonal 8200
The tops of the base of a regular hexagonal pyramid lie on a circle with a radius of 10 cm. The height of the pyramid is 12cm. What is its volume? - Rectangle - parallelogram
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - Ratio of squares
A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares?
- Pentagon
Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm. - Motion on circle
The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate. - Calculate 2577
Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm. - Deformation 6260
The carpet is wound on a cardboard roll in the shape of a cylinder with a diameter of d=12cm and a length of l=2m. The rolled-up carpet has an outer diameter of D=38cm, and the thickness of the rug is 8mm. What area can the carpet cover after unfolding? D - Sphere in cone
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
- From plasticine
Michael modeled from plasticine a 15 cm high pyramid with a rectangular base, with the sides of the base a = 12 cm and b = 8 cm. From this pyramid, Janka modeled a rotating cone with a base diameter of 10 cm. How tall was Janka's cone? - Chord MN
Chord MN of the circle has distance from the center circle S 120 cm. Angle MSN is 64°. Determine the radius of the circle. - Costume
Denisa is preparing for a goldsmith's costume carnival. During the preparations, she thought she would let her hair wipe instead - she would apply a 5 μm thick layer of gold to each hair. How much gold would Denisa need? Assume that all hundred thousand D - Pentagonal prism
The regular pentagonal prism is 10 cm high. The radius of the circle of the described base is 8 cm. Calculate the volume and surface area of the prism. - Hexagon rotation
A regular hexagon of side 6 cm is rotated at 60° along a line passing through its longest diagonal. What is the volume of the figure thus generated?
- 2d shape
Calculate the area of a shape in which an arbitrary point is not more than 3 cm from the segment AB. The length of segment AB is 5 cm. - Park
Rotating sprayer irrigation lawns will permanently surround the newly built park. Find the largest radius of the circle that can be irrigated by sprayer P, not to spray park visitors online AB. Distance AB = 55 m, AP = 36 m and BP = 28 m. - Circular 7894
A 2 cm thick layer of ice formed in the circular water tank. What part of the tank's water (answer in percent) froze if the tank has a diameter of 20 m and a depth of 1.5 m? - Corresponding 82704
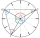On the circular face of the clock, we connect the points corresponding to the numbers 2, 5, and 9 to each other, which creates a triangle. Calculate the sizes of all interior angles. - Estate
Semicircle estate must be a fence. The straight section has a 32 meters long fence. How many meters of the fence should we buy?
Construct a trapezoid if b = 4cm, c = 7cm, d = 4,5cm, v = 3 cm (Procedure, discussion, sketch, analysis, construction)Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
