Area + line segment - practice problems
Number of problems found: 24
- PQR - Euclid
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - The volume 8
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Quadrilateral 82616
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the area of quadrilateral AFHD. - Respectively 81293
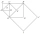The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help...
- Distances 79974
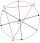The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be - Calculate 58953
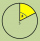Calculate the area of a circular line if the radius r = 80 cm and the central angle is α = 110 °. - Construction 32971
There is any circle k that does not have a marked center. Use a suitable construction to find the center of the circle k. Try on two different circles. - Coordinates
Determine the coordinates of the vertices and the area of the parallelogram, the two sides of which lie on the lines 8x + 3y + 1 = 0, 2x + y-1 = 0, and the diagonal on the line 3x + 2y + 3 = 0 - Circumference 26361
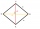The ABCD diamond has a circumference of 72 cm. The longer diagonal of the animal with the line segment AB angle is 30 °. Calculate the area of the ABCD diamond.
- A cell tower
A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal? - Hexagon
Divide a regular hexagon into lines with nine completely identical parts; none of them must be in a mirror image (you can only rotate individual parts arbitrarily). - Diagonals at right angle
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - MO Z8–I–6 2018
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Right triangle from axes
A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment?
- Distance 6164
What is the area of a square when the distance between parallel lines is 6? - Trapezoid - intersection of diagonals
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area. - triangle 5420
Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl - Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Rectangular trapezoid
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid.
Calculate the area of a shape in which an arbitrary point is not more than 3 cm from the segment AB. The length of segment AB is 5 cm.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
