Triangle + line segment - practice problems
Number of problems found: 60
- Triangles - segments
How many triangles can be formed with segments measuring one and 2/3 mm one 3/4 mm and 2 1/2 mm - PQR - Euclid
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Line segment
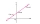Find the length of the line joining points A(-4,8) and B(-1,4). - Angle and slope
Find the angle between the x-axis and the line joining the points (3, -1) and (4,-2) .
- The volume 8
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Four points
There are 4 nonlinear points. How many triangles can form by joining them? - Right-angled 3147
In a right-angled triangle ABC, the height of side c has a length of 6 cm. The letter D indicates the heel of the height. Line segment AD is 8 cm long. Calculate the area of triangle ABC. ( example on Monitor 9 ) - Railway
The railway line had a 5.8 km segment climb nine permille. How many meters does the track ascent? - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
- Internal angles
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Three points 2
The three points are A(3, 8), B(6, 2), and C(10, 2). Point D is such that the line DA is perpendicular to AB, and DC is parallel to AB. Calculate the coordinates of D. - Construct 8
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati - Similarity coefficient
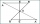In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other. - Intersection 7247
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin
- Determined 3488
Find out if there is a triangle whose two sides are 5 cm and 8 cm long and the middle bar determined by their centers is 1.5 cm long. - Right angled triangle 2
LMN is a right-angled triangle with vertices at L(1,3), M(3,5), and N(6,n). Given angle LMN is 90° find n - Sides of the triangle
The sides of the triangle ABC have a length of 4 cm, 5 cm, and 7 cm. Construct triangle A'B'C', similar to triangle ABC, which has a circumference of 12 cm. - Distances 79974
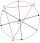The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be - Three points
Three points: A (-3;-5), B (9;-10), and C (2;k). AB=AC What is the value of k?
A line segment AA1 of length 6 cm is given. Construct all triangles ABC for which AA1 is the hypotenuse, side length BC is 5 cm, and angle gamma is 60°.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
