Angle + the proof - practice problems
Number of problems found: 8
- Triangle P2
Can a triangle have two right angles? - Isosceles triangle and cosine
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α. - Bisector 2
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - Laws
From which law directly follows the validity of Pythagoras' theorem in the right triangle? ...
- Triangle 80994
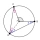In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify. - Sum of inner angles
Prove that the sum of all inner angles of any convex n-angle equals (n-2).180 degrees. - Diagonal in rectangle
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - Constructed 77874
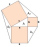Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same.
We apologize, but in this category are not a lot of examples.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
