Angle + similarity of triangles - practice problems - page 2 of 4
Number of problems found: 63
- Angle in RT
Determine the size of the smallest internal angle of a right triangle whose sides constitute the sizes of consecutive members of arithmetic progressions. - Isosceles 67744
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle. - Shadow 7838
A man 1.65 m tall casts a shadow of 1.25 m. How tall is the tree whose shadow is in debt 2.58 m? - Similarity
Are two right triangles similar if the first one has an acute angle 60° and the second one has an acute angle 30°?
- Triangles 83634
We have similar triangles ABC with angle CAB=45° and angle ACB= 30° and a similar triangle OPN. What is the angle NOP in a similar triangle? - Triangles 6682
Triangles ABC and A'B'C'. They are similar. In triangle ABC, the measures of the two angles are 25 degrees and 65 degrees. Explain why, in triangle A'B'C', the sum of the sizes of the two angles is equal to 90 degrees. - Cosine
Calculate the cosine of the smallest internal angle in a right-angled triangle with cathetus 3 and 8 and the hypotenuse 8.544. - The triangles
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - Two angles
The triangles ABC and A'B'C 'are similar. In the ABC triangle, the two angles are 25° and 65°. Explain why in the triangle A'B'C 'is the sum of two angles of 90 degrees.
- Triangles 6647 For triangles ABC and A'B'C': alpha = alpha with a line, beta with line = beta. a) are these triangles identical? Why? b) are these triangles similar? Why?
- Similarity coefficient
The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'. - Right-angled triangle
The right-angled triangle XYZ is similar to the triangle ABC, which has a right angle at the vertex X. The following applies: side a = 9 cm, x=4 cm, x = v-4 (v = height of triangle ABC). Calculate the unknown side lengths of both triangles. - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°. - Right-angled 80745
The area of a right-angled triangle KLM with a right angle at the vertex L is 60 mm square, and its hypotenuse k is 10 mm long. Triangles KLM and RST are similar. The similarity ratio is k=2.5. Calculate the area of triangle RST.
- The truncated
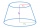The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm, and height v = 5 cm. What is the volume of the cone from which the truncated cone originated? - Railways
Railways climb 2.8 ‰. Calculate the height difference between two points on the railway distant 5997 meters. - Coefficient 6672
In the triangle ABC is [AB] = 20cm, [BC] = 10cm, A = 30 °. Construct a triangle A'B'C' similar to triangle ABC if the similarity coefficient is 0.5 - Garage
There are two laths in the garage opposite one another: one 2 meters long and the second 3 meters long. They fall against each other and stay against the opposite walls of the garage. Both laths cross 70 cm above the garage floor. How wide is the garage? - Diagonal in rectangle
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts.
At a distance of 10 m from the river bank, they measured the base AB = 50 m parallel to the bank. Point C on the other bank of the river is visible from point A at an angle of 32°30' and from point B at an angle of 42°15'. Calculate the width of the riverDo you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
