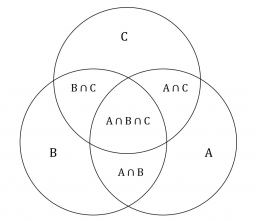
Probability of intersection
Three students have a probability of 0.7,0.5, and 0.4 to graduate from university, respectively. What is the probability that at least one of them will be graduated?
Final Answer:
Tips for related online calculators
Would you like to compute the count of combinations?
You need to know the following knowledge to solve this word math problem:
combinatoricsalgebrabasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Honor graduate percentage
As many as 62.5% of residents at the business academy graduated with honors. How many high school graduates would there be if 30 students graduated with honors? - The accompanying
The accompanying table gives the probability distribution of the number of courses randomly selected student has registered Number of courses 1 2 3 4 5 6 7 Probability 0.02 0.03 0.1 0.3 0.4 - 0.01 respectively. a) Find the probability of a student registe - Three students
Three students independently try to solve the problem. The first student will solve a similar problem with a probability of 0.6, the second student will solve at a probability of 0.55, and the third will solve at a probability of 0.04. The problem is reso - Flu probability
In the monitored group of people, 8% are ill with the flu. One hundred people from this group were examined. What is the probability that at most 5 of them will be sick with the flu? (round to 3 decimal places) - Lottery
Pavol has two lottery tickets, each from the other lottery. In the first is 1203 000 lottery tickets from them wins 410 000, the second has 1478 000 lottery tickets from them wins 1478 000 tickets. What is the probability that at least one Pavol's ticket - Competition in the class
There are 10 students in the class, of which 8 are girls and two are boys. We want to select three for the competition. What is the probability that they will be: a) 2 girls and 1 boy b) 1 girl and 2 boys c) 3 girls d) 3 boys e) at least 2 girls - In class 24
There are a total of 16 students in the class, a quarter of whom are girls. We randomly select a team of five. Determine the probability that the team will have: a) at least 4 girls. b) at most 1 girl. c) no girls.
