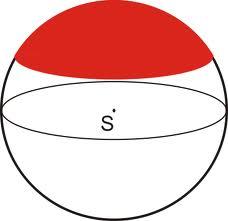
Spherical cap
From the sphere with a radius of 21 was a truncated spherical cap. Its height is 6. What part of the volume is a spherical cap from the whole sphere?
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Spherical tank
The water tower tank is a sphere with a radius of 35ft. If the tank is filled to one-quarter full, what is the height of the water? - Sphere - parts
Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 10 cm and a height v = 3.4 cm. - Calculate 65354
Calculate the surface of a spherical paragraph with a height of 6 cm and a radius of 15 cm - Stadium
A domed stadium is shaped like a spherical segment with a base radius of 150 m. The dome must contain a volume of 3500000 m³. Determine the dome's height at its center to the nearest tenth of a meter.
- Spherical cap
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap. - Sphere cut
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - Spherical segment
The spherical segment with height h=2 has a volume of V=112. Calculate the radius of the sphere which is cut in this segment.
