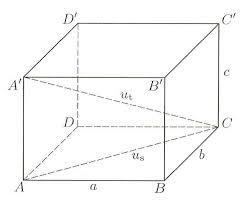
Cube diagonals
If you know the length of the body diagonal u = 216 cm, determine the cube's volume and surface area.
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Cube from Body Diagonal
Find the volume and surface area of a cube whose space diagonal has length u = 216 cm. - Cube diagonals
Determine the length of the body and wall diagonals of the cube, the volume of which is equal to 0.343 decimetres. Also, calculate its surface. - Cube wall Calculate the cube's diagonal if you know that one wall's surface equals 36 centimeters square. Please also calculate its volume.
- Cubes
A sphere is inscribed in one cube and the same sphere is circumscribed about another cube. Calculate the difference between the volumes of the two cubes if the difference between their surface areas is 231 cm². - Cube edge ratio
The lengths of the edges of two cubes are in the ratio 1:2, determine: a) the ratio of the area of the wall of the smaller cube to the area of the wall of the larger cube. b) the ratio of the surface of the smaller cube to the surface of the larger cube. - Cube diagonals
Determine the wall and body diagonal of the cube, with the surface of one of its walls being 121 square centimeters. - Three cubes
The body was created by gluing three identical cubes. Its volume is 192 cm³. What is its surface in dm²?
