Square and circles
The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a.
Your answer:
Your answer:
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Equilateral triangle v3
Find the area of the colored gray part. An equilateral triangle has a side length of 8 cm. Arc centers are the vertices of a triangle. - Eq triangle minus arcs
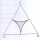In an equilateral triangle with a 2 cm long side, the arcs of three circles are drawn from the centers at the vertices and radii 1 cm. Calculate the area of the shaded part - a formation that makes up the difference between the triangle area and circular - Recursion squares
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri - Colored area
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s - Square colored percentage
The square in the picture has a side length of 6 cm. What percentage of the area is the colored part? - Inscribed triangle
A circle is an inscribed triangle, and its vertices divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle. - Circle arc segment
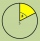A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
