An equilateral
An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Cross-section 47131
The 5 m long bar has a cross-section of an equilateral triangle with a side of 35 mm. Calculate its volume - Difference 66354
A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle. - Infinity
A square with a side 19 long is an inscribed circle, and the circle is inscribed next to the square, circle, and so on to infinity. Calculate the sum of the area of all these squares. - Equilateral 80573
The field has the shape of an equilateral triangle. Calculate its area if you know that the side is 280 meters long.
- Determine 82724
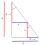A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the area of this square. - ET inscribed circle
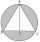An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - Recursion squares
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri
