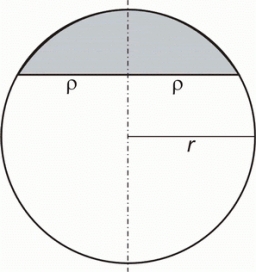
Hemisphere cut
Calculate the spherical layer's volume that remains from the hemisphere after the 3 cm section is cut. The height of the hemisphere is 10 cm.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- sphere
- spherical cap
- spherical segment
- hemisphere
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Paragraphs 69164
 What is the volume of the spherical layer that remains after cutting the paragraphs on both sides of the ball, whose height is 3.5 cm? Is the diameter of the ball 24 cm?
What is the volume of the spherical layer that remains after cutting the paragraphs on both sides of the ball, whose height is 3.5 cm? Is the diameter of the ball 24 cm? - Hemisphere 70054
 Find the volume of the spherical layer that results from a hemisphere with a radius of 5 cm by cutting a paragraph whose height is 1.5 cm.
Find the volume of the spherical layer that results from a hemisphere with a radius of 5 cm by cutting a paragraph whose height is 1.5 cm. - Calculate sphere cap
 Calculate the surface of a spherical cap with a height of 6 cm and a radius of 15 cm
Calculate the surface of a spherical cap with a height of 6 cm and a radius of 15 cm - Spherical section cut
 Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
- Hemispherical hollow
 The vessel's hemispherical hollow is filled with water to a height of 10 cm =. How many liters of water are inside if the hollow's inside diameter is d = 28cm?
The vessel's hemispherical hollow is filled with water to a height of 10 cm =. How many liters of water are inside if the hollow's inside diameter is d = 28cm? - A spherical segment
 The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface.
The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface. - Spherical cap
 Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
