Equilateral 14873
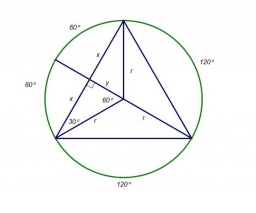
There is a circle with a radius of 2.5 cm and point A, which lies on it. Write an equilateral triangle ABC in the circle.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Two chords
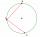There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure. - Convex angle
There is a circle k (S; r), and a point A, which lies on this circle. There is also a point B on the circumference, for which it is true that in one direction, it is five times further from point A than in the opposite direction (around the circumference - Circle
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - Circle inscribed
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
- Conditions 7186
Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Equilateral triangle ABC
In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl - Circle
The circle k with diameter |MN| = 61. Point J lies on the circle k. Line |MJ|=22. Calculate the length of a segment JN.
