Quadrilateral
In the square ABCD point, P is in the middle of the DC side, and point Q is in the middle of side AD. If the area of quadrilateral BQPC is 76 cm2, what is the area of ABCD?
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrilateral 67384
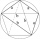Construct a quadrilateral ABCD if AB = 10cm, AD = 6cm, DC = 6.5cm and angle BCD = 90 degrees - Tunnel - quadrilateral
How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral. - Triangle ABP
An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP. - Quadrilateral 80729
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Quadrilateral 66614
The picture shows a square ABCD with the center S and the side 8 cm long. Point E is any point on the CD side other than C and D. Calculate the area of the ASBE quadrilateral in cm². - Construct diagonals
The point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of the rect - Katy MO
Kate drew a triangle ABC. The middle of the line segment AB is marked as X, and the center of the side AC is marked as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximall
