Complex number calculator
There are 24 solutions, due to “The Fundamental Theorem of Algebra”. Your expression contains roots of complex numbers or powers to 1/n.
z1 = ((-5i)^(1/8))*(8^(1/3)) = 2.3986959-0.4771303i = 2.4456891 × ei -0.1963495 = 2.4456891 × ei (-0.0625) π Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei -0.1963495 = 1.2228445 × ei (-0.0625) π = 1.1993479-0.2385651i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = 2
- Multiple: the result of step No. 2 * the result of step No. 4 = (1.1993479-0.2385651i) * 2 = 2.3986959-0.4771303i
The result z1
Rectangular form (standard form):
z = 2.3986959-0.4771303i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -11°15'
Polar form:
z = 2.4456891 × (cos (-11°15') + i sin (-11°15'))
Exponential form:
z = 2.4456891 × ei -0.1963495 = 2.4456891 × ei (-0.0625) π
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -0.1963495 rad = -11.25° = -11°15' = -0.0625π rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.3986959-0.4771303i
Real part: x = Re z = 2.399
Imaginary part: y = Im z = -0.47713027
z = 2.3986959-0.4771303i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -11°15'
Polar form:
z = 2.4456891 × (cos (-11°15') + i sin (-11°15'))
Exponential form:
z = 2.4456891 × ei -0.1963495 = 2.4456891 × ei (-0.0625) π
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -0.1963495 rad = -11.25° = -11°15' = -0.0625π rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.3986959-0.4771303i
Real part: x = Re z = 2.399
Imaginary part: y = Im z = -0.47713027
z2 = ((-5i)^(1/8))*(8^(1/3)) = 2.0335162+1.3587521i = 2.4456891 × ei 3π/16 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 3π/16 = 1.0167581+0.679376i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = 2
- Multiple: the result of step No. 2 * the result of step No. 4 = (1.0167581+0.679376i) * 2 = 2.0335162+1.3587521i
The result z2
Rectangular form (standard form):
z = 2.0335162+1.3587521i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 33°45'
Polar form:
z = 2.4456891 × (cos 33°45' + i sin 33°45')
Exponential form:
z = 2.4456891 × ei 0.5890486 = 2.4456891 × ei 3π/16
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 0.5890486 rad = 33.75° = 33°45' = 0.1875π = 3π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.0335162+1.3587521i
Real part: x = Re z = 2.034
Imaginary part: y = Im z = 1.35875206
z = 2.0335162+1.3587521i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 33°45'
Polar form:
z = 2.4456891 × (cos 33°45' + i sin 33°45')
Exponential form:
z = 2.4456891 × ei 0.5890486 = 2.4456891 × ei 3π/16
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 0.5890486 rad = 33.75° = 33°45' = 0.1875π = 3π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.0335162+1.3587521i
Real part: x = Re z = 2.034
Imaginary part: y = Im z = 1.35875206
z3 = ((-5i)^(1/8))*(8^(1/3)) = 0.4771303+2.3986959i = 2.4456891 × ei 7π/16 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 7π/16 = 0.2385651+1.1993479i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = 2
- Multiple: the result of step No. 2 * the result of step No. 4 = (0.2385651+1.1993479i) * 2 = 0.4771303+2.3986959i
The result z3
Rectangular form (standard form):
z = 0.4771303+2.3986959i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 78°45'
Polar form:
z = 2.4456891 × (cos 78°45' + i sin 78°45')
Exponential form:
z = 2.4456891 × ei 1.3744468 = 2.4456891 × ei 7π/16
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 1.3744468 rad = 78.75° = 78°45' = 0.4375π = 7π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 0.4771303+2.3986959i
Real part: x = Re z = 0.477
Imaginary part: y = Im z = 2.39869586
z = 0.4771303+2.3986959i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 78°45'
Polar form:
z = 2.4456891 × (cos 78°45' + i sin 78°45')
Exponential form:
z = 2.4456891 × ei 1.3744468 = 2.4456891 × ei 7π/16
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 1.3744468 rad = 78.75° = 78°45' = 0.4375π = 7π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 0.4771303+2.3986959i
Real part: x = Re z = 0.477
Imaginary part: y = Im z = 2.39869586
z4 = ((-5i)^(1/8))*(8^(1/3)) = -1.3587521+2.0335162i = 2.4456891 × ei 11π/16 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 11π/16 = -0.679376+1.0167581i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = 2
- Multiple: the result of step No. 2 * the result of step No. 4 = (-0.679376+1.0167581i) * 2 = -1.3587521+2.0335162i
The result z4
Rectangular form (standard form):
z = -1.3587521+2.0335162i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 123°45'
Polar form:
z = 2.4456891 × (cos 123°45' + i sin 123°45')
Exponential form:
z = 2.4456891 × ei 2.1598449 = 2.4456891 × ei 11π/16
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 2.1598449 rad = 123.75° = 123°45' = 0.6875π = 11π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -1.3587521+2.0335162i
Real part: x = Re z = -1.359
Imaginary part: y = Im z = 2.03351616
z = -1.3587521+2.0335162i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 123°45'
Polar form:
z = 2.4456891 × (cos 123°45' + i sin 123°45')
Exponential form:
z = 2.4456891 × ei 2.1598449 = 2.4456891 × ei 11π/16
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 2.1598449 rad = 123.75° = 123°45' = 0.6875π = 11π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -1.3587521+2.0335162i
Real part: x = Re z = -1.359
Imaginary part: y = Im z = 2.03351616
z5 = ((-5i)^(1/8))*(8^(1/3)) = -2.3986959+0.4771303i = 2.4456891 × ei 15π/16 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 15π/16 = -1.1993479+0.2385651i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = 2
- Multiple: the result of step No. 2 * the result of step No. 4 = (-1.1993479+0.2385651i) * 2 = -2.3986959+0.4771303i
The result z5
Rectangular form (standard form):
z = -2.3986959+0.4771303i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 168°45'
Polar form:
z = 2.4456891 × (cos 168°45' + i sin 168°45')
Exponential form:
z = 2.4456891 × ei 2.9452431 = 2.4456891 × ei 15π/16
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 2.9452431 rad = 168.75° = 168°45' = 0.9375π = 15π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.3986959+0.4771303i
Real part: x = Re z = -2.399
Imaginary part: y = Im z = 0.47713027
z = -2.3986959+0.4771303i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 168°45'
Polar form:
z = 2.4456891 × (cos 168°45' + i sin 168°45')
Exponential form:
z = 2.4456891 × ei 2.9452431 = 2.4456891 × ei 15π/16
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 2.9452431 rad = 168.75° = 168°45' = 0.9375π = 15π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.3986959+0.4771303i
Real part: x = Re z = -2.399
Imaginary part: y = Im z = 0.47713027
z6 = ((-5i)^(1/8))*(8^(1/3)) = -2.0335162-1.3587521i = 2.4456891 × ei (-13π/16) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-13π/16) = -1.0167581-0.679376i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = 2
- Multiple: the result of step No. 2 * the result of step No. 4 = (-1.0167581-0.679376i) * 2 = -2.0335162-1.3587521i
The result z6
Rectangular form (standard form):
z = -2.0335162-1.3587521i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -146°15'
Polar form:
z = 2.4456891 × (cos (-146°15') + i sin (-146°15'))
Exponential form:
z = 2.4456891 × ei -2.552544 = 2.4456891 × ei (-13π/16)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -2.552544 rad = -146.25° = -146°15' = -0.8125π = -13π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.0335162-1.3587521i
Real part: x = Re z = -2.034
Imaginary part: y = Im z = -1.35875206
z = -2.0335162-1.3587521i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -146°15'
Polar form:
z = 2.4456891 × (cos (-146°15') + i sin (-146°15'))
Exponential form:
z = 2.4456891 × ei -2.552544 = 2.4456891 × ei (-13π/16)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -2.552544 rad = -146.25° = -146°15' = -0.8125π = -13π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.0335162-1.3587521i
Real part: x = Re z = -2.034
Imaginary part: y = Im z = -1.35875206
z7 = ((-5i)^(1/8))*(8^(1/3)) = -0.4771303-2.3986959i = 2.4456891 × ei (-9π/16) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-9π/16) = -0.2385651-1.1993479i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = 2
- Multiple: the result of step No. 2 * the result of step No. 4 = (-0.2385651-1.1993479i) * 2 = -0.4771303-2.3986959i
The result z7
Rectangular form (standard form):
z = -0.4771303-2.3986959i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -101°15'
Polar form:
z = 2.4456891 × (cos (-101°15') + i sin (-101°15'))
Exponential form:
z = 2.4456891 × ei -1.7671459 = 2.4456891 × ei (-9π/16)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -1.7671459 rad = -101.25° = -101°15' = -0.5625π = -9π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -0.4771303-2.3986959i
Real part: x = Re z = -0.477
Imaginary part: y = Im z = -2.39869586
z = -0.4771303-2.3986959i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -101°15'
Polar form:
z = 2.4456891 × (cos (-101°15') + i sin (-101°15'))
Exponential form:
z = 2.4456891 × ei -1.7671459 = 2.4456891 × ei (-9π/16)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -1.7671459 rad = -101.25° = -101°15' = -0.5625π = -9π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -0.4771303-2.3986959i
Real part: x = Re z = -0.477
Imaginary part: y = Im z = -2.39869586
z8 = ((-5i)^(1/8))*(8^(1/3)) = 1.3587521-2.0335162i = 2.4456891 × ei (-5π/16) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-5π/16) = 0.679376-1.0167581i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = 2
- Multiple: the result of step No. 2 * the result of step No. 4 = (0.679376-1.0167581i) * 2 = 1.3587521-2.0335162i
The result z8
Rectangular form (standard form):
z = 1.3587521-2.0335162i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -56°15'
Polar form:
z = 2.4456891 × (cos (-56°15') + i sin (-56°15'))
Exponential form:
z = 2.4456891 × ei -0.9817477 = 2.4456891 × ei (-5π/16)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -0.9817477 rad = -56.25° = -56°15' = -0.3125π = -5π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 1.3587521-2.0335162i
Real part: x = Re z = 1.359
Imaginary part: y = Im z = -2.03351616
z = 1.3587521-2.0335162i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -56°15'
Polar form:
z = 2.4456891 × (cos (-56°15') + i sin (-56°15'))
Exponential form:
z = 2.4456891 × ei -0.9817477 = 2.4456891 × ei (-5π/16)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -0.9817477 rad = -56.25° = -56°15' = -0.3125π = -5π/16 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 1.3587521-2.0335162i
Real part: x = Re z = 1.359
Imaginary part: y = Im z = -2.03351616
z9 = ((-5i)^(1/8))*(8^(1/3)) = -0.786141+2.3158967i = 2.4456891 × ei 29π/48 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei -0.1963495 = 1.2228445 × ei (-0.0625) π = 1.1993479-0.2385651i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1+1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (1.1993479-0.2385651i) * (-1+1.7320508i) = 1.19934793 * (-1) + 1.19934793 * 1.7320508076i + (-0.2385651361i) * (-1) + (-0.2385651361i) * 1.7320508076i = -1.19934793+2.07733155i+0.23856514i-0.41320694i2 = -1.19934793+2.07733155i+0.23856514i+0.41320694 = -1.19934793 0.413207 +i(2.07733155 + 0.238565) = -0.786141+2.3158967ialternative steps1.2228445 × ei -0.1963495 = 1.2228445 × ei (-0.0625) π × 2 × ei 2π/3 = 1.2228445 × 2 × ei ((-0.0625)+2π/3) = 2.4456891 × ei 29π/48 = -0.786141+2.3158967i
The result z9
Rectangular form (standard form):
z = -0.786141+2.3158967i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 108°45'
Polar form:
z = 2.4456891 × (cos 108°45' + i sin 108°45')
Exponential form:
z = 2.4456891 × ei 1.8980456 = 2.4456891 × ei 29π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 1.8980456 rad = 108.75° = 108°45' = 0.6041667π = 29π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -0.786141+2.3158967i
Real part: x = Re z = -0.786
Imaginary part: y = Im z = 2.31589669
z = -0.786141+2.3158967i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 108°45'
Polar form:
z = 2.4456891 × (cos 108°45' + i sin 108°45')
Exponential form:
z = 2.4456891 × ei 1.8980456 = 2.4456891 × ei 29π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 1.8980456 rad = 108.75° = 108°45' = 0.6041667π = 29π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -0.786141+2.3158967i
Real part: x = Re z = -0.786
Imaginary part: y = Im z = 2.31589669
z10 = ((-5i)^(1/8))*(8^(1/3)) = -2.1934719+1.0817006i = 2.4456891 × ei 41π/48 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 3π/16 = 1.0167581+0.679376i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1+1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (1.0167581+0.679376i) * (-1+1.7320508i) = 1.0167580798154 * (-1) + 1.0167580798154 * 1.7320508076i + 0.67937602882697i * (-1) + 0.67937602882697i * 1.7320508076i = -1.01675808+1.76107665i-0.67937603i+1.1767138i2 = -1.01675808+1.76107665i-0.67937603i-1.1767138 = -1.01675808- 1.176714 +i(1.76107665 - 0.679376) = -2.1934719+1.0817006ialternative steps1.2228445 × ei 3π/16 × 2 × ei 2π/3 = 1.2228445 × 2 × ei (3π/16+2π/3) = 2.4456891 × ei 41π/48 = -2.1934719+1.0817006i
The result z10
Rectangular form (standard form):
z = -2.1934719+1.0817006i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 153°45'
Polar form:
z = 2.4456891 × (cos 153°45' + i sin 153°45')
Exponential form:
z = 2.4456891 × ei 2.6834437 = 2.4456891 × ei 41π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 2.6834437 rad = 153.75° = 153°45' = 0.8541667π = 41π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.1934719+1.0817006i
Real part: x = Re z = -2.193
Imaginary part: y = Im z = 1.08170062
z = -2.1934719+1.0817006i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 153°45'
Polar form:
z = 2.4456891 × (cos 153°45' + i sin 153°45')
Exponential form:
z = 2.4456891 × ei 2.6834437 = 2.4456891 × ei 41π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 2.6834437 rad = 153.75° = 153°45' = 0.8541667π = 41π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.1934719+1.0817006i
Real part: x = Re z = -2.193
Imaginary part: y = Im z = 1.08170062
z11 = ((-5i)^(1/8))*(8^(1/3)) = -2.3158967-0.786141i = 2.4456891 × ei (-43π/48) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 7π/16 = 0.2385651+1.1993479i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1+1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (0.2385651+1.1993479i) * (-1+1.7320508i) = 0.2385651361 * (-1) + 0.2385651361 * 1.7320508076i + 1.19934793i * (-1) + 1.19934793i * 1.7320508076i = -0.23856514+0.41320694i-1.19934793i+2.07733155i2 = -0.23856514+0.41320694i-1.19934793i-2.07733155 = -0.23856514- 2.077332 +i(0.41320694 - 1.199348) = -2.3158967-0.786141ialternative steps1.2228445 × ei 7π/16 × 2 × ei 2π/3 = 1.2228445 × 2 × ei (7π/16+2π/3) = 2.4456891 × ei (-43π/48) = -2.3158967-0.786141i
The result z11
Rectangular form (standard form):
z = -2.3158967-0.786141i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -161°15'
Polar form:
z = 2.4456891 × (cos (-161°15') + i sin (-161°15'))
Exponential form:
z = 2.4456891 × ei -2.8143434 = 2.4456891 × ei (-43π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -2.8143434 rad = -161.25° = -161°15' = -0.8958333π = -43π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.3158967-0.786141i
Real part: x = Re z = -2.316
Imaginary part: y = Im z = -0.78614099
z = -2.3158967-0.786141i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -161°15'
Polar form:
z = 2.4456891 × (cos (-161°15') + i sin (-161°15'))
Exponential form:
z = 2.4456891 × ei -2.8143434 = 2.4456891 × ei (-43π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -2.8143434 rad = -161.25° = -161°15' = -0.8958333π = -43π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.3158967-0.786141i
Real part: x = Re z = -2.316
Imaginary part: y = Im z = -0.78614099
z12 = ((-5i)^(1/8))*(8^(1/3)) = -1.0817006-2.1934719i = 2.4456891 × ei (-31π/48) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 11π/16 = -0.679376+1.0167581i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1+1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (-0.679376+1.0167581i) * (-1+1.7320508i) = -0.67937602882697 * (-1) + (-0.67937602882697) * 1.7320508076i + 1.0167580798154i * (-1) + 1.0167580798154i * 1.7320508076i = 0.67937603-1.1767138i-1.01675808i+1.76107665i2 = 0.67937603-1.1767138i-1.01675808i-1.76107665 = 0.67937603- 1.761077 +i(-1.1767138 - 1.016758) = -1.0817006-2.1934719ialternative steps1.2228445 × ei 11π/16 × 2 × ei 2π/3 = 1.2228445 × 2 × ei (11π/16+2π/3) = 2.4456891 × ei (-31π/48) = -1.0817006-2.1934719i
The result z12
Rectangular form (standard form):
z = -1.0817006-2.1934719i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -116°15'
Polar form:
z = 2.4456891 × (cos (-116°15') + i sin (-116°15'))
Exponential form:
z = 2.4456891 × ei -2.0289453 = 2.4456891 × ei (-31π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -2.0289453 rad = -116.25° = -116°15' = -0.6458333π = -31π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -1.0817006-2.1934719i
Real part: x = Re z = -1.082
Imaginary part: y = Im z = -2.19347188
z = -1.0817006-2.1934719i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -116°15'
Polar form:
z = 2.4456891 × (cos (-116°15') + i sin (-116°15'))
Exponential form:
z = 2.4456891 × ei -2.0289453 = 2.4456891 × ei (-31π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -2.0289453 rad = -116.25° = -116°15' = -0.6458333π = -31π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -1.0817006-2.1934719i
Real part: x = Re z = -1.082
Imaginary part: y = Im z = -2.19347188
z13 = ((-5i)^(1/8))*(8^(1/3)) = 0.786141-2.3158967i = 2.4456891 × ei (-19π/48) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 15π/16 = -1.1993479+0.2385651i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1+1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (-1.1993479+0.2385651i) * (-1+1.7320508i) = -1.19934793 * (-1) + (-1.19934793) * 1.7320508076i + 0.2385651361i * (-1) + 0.2385651361i * 1.7320508076i = 1.19934793-2.07733155i-0.23856514i+0.41320694i2 = 1.19934793-2.07733155i-0.23856514i-0.41320694 = 1.19934793- 0.413207 +i(-2.07733155 - 0.238565) = 0.786141-2.3158967ialternative steps1.2228445 × ei 15π/16 × 2 × ei 2π/3 = 1.2228445 × 2 × ei (15π/16+2π/3) = 2.4456891 × ei (-19π/48) = 0.786141-2.3158967i
The result z13
Rectangular form (standard form):
z = 0.786141-2.3158967i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -71°15'
Polar form:
z = 2.4456891 × (cos (-71°15') + i sin (-71°15'))
Exponential form:
z = 2.4456891 × ei -1.2435471 = 2.4456891 × ei (-19π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -1.2435471 rad = -71.25° = -71°15' = -0.3958333π = -19π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 0.786141-2.3158967i
Real part: x = Re z = 0.786
Imaginary part: y = Im z = -2.31589669
z = 0.786141-2.3158967i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -71°15'
Polar form:
z = 2.4456891 × (cos (-71°15') + i sin (-71°15'))
Exponential form:
z = 2.4456891 × ei -1.2435471 = 2.4456891 × ei (-19π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -1.2435471 rad = -71.25° = -71°15' = -0.3958333π = -19π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 0.786141-2.3158967i
Real part: x = Re z = 0.786
Imaginary part: y = Im z = -2.31589669
z14 = ((-5i)^(1/8))*(8^(1/3)) = 2.1934719-1.0817006i = 2.4456891 × ei (-7π/48) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-13π/16) = -1.0167581-0.679376i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1+1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (-1.0167581-0.679376i) * (-1+1.7320508i) = -1.0167580798154 * (-1) + (-1.0167580798154) * 1.7320508076i + (-0.67937602882697i) * (-1) + (-0.67937602882697i) * 1.7320508076i = 1.01675808-1.76107665i+0.67937603i-1.1767138i2 = 1.01675808-1.76107665i+0.67937603i+1.1767138 = 1.01675808 1.176714 +i(-1.76107665 + 0.679376) = 2.1934719-1.0817006ialternative steps1.2228445 × ei (-13π/16) × 2 × ei 2π/3 = 1.2228445 × 2 × ei ((-13π/16)+2π/3) = 2.4456891 × ei (-7π/48) = 2.1934719-1.0817006i
The result z14
Rectangular form (standard form):
z = 2.1934719-1.0817006i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -26°15'
Polar form:
z = 2.4456891 × (cos (-26°15') + i sin (-26°15'))
Exponential form:
z = 2.4456891 × ei -0.4581489 = 2.4456891 × ei (-7π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -0.4581489 rad = -26.25° = -26°15' = -0.1458333π = -7π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.1934719-1.0817006i
Real part: x = Re z = 2.193
Imaginary part: y = Im z = -1.08170062
z = 2.1934719-1.0817006i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -26°15'
Polar form:
z = 2.4456891 × (cos (-26°15') + i sin (-26°15'))
Exponential form:
z = 2.4456891 × ei -0.4581489 = 2.4456891 × ei (-7π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -0.4581489 rad = -26.25° = -26°15' = -0.1458333π = -7π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.1934719-1.0817006i
Real part: x = Re z = 2.193
Imaginary part: y = Im z = -1.08170062
z15 = ((-5i)^(1/8))*(8^(1/3)) = 2.3158967+0.786141i = 2.4456891 × ei 0.3272492 = 2.4456891 × ei 0.1041667 π Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-9π/16) = -0.2385651-1.1993479i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1+1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (-0.2385651-1.1993479i) * (-1+1.7320508i) = -0.2385651361 * (-1) + (-0.2385651361) * 1.7320508076i + (-1.19934793i) * (-1) + (-1.19934793i) * 1.7320508076i = 0.23856514-0.41320694i+1.19934793i-2.07733155i2 = 0.23856514-0.41320694i+1.19934793i+2.07733155 = 0.23856514 2.077332 +i(-0.41320694 + 1.199348) = 2.3158967+0.786141ialternative steps1.2228445 × ei (-9π/16) × 2 × ei 2π/3 = 1.2228445 × 2 × ei ((-9π/16)+2π/3) = 2.4456891 × ei 0.3272492 = 2.4456891 × ei 0.1041667 π = 2.3158967+0.786141i
The result z15
Rectangular form (standard form):
z = 2.3158967+0.786141i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 18°45'
Polar form:
z = 2.4456891 × (cos 18°45' + i sin 18°45')
Exponential form:
z = 2.4456891 × ei 0.3272492 = 2.4456891 × ei 0.1041667 π
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 0.3272492 rad = 18.75° = 18°45' = 0.1041667π rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.3158967+0.786141i
Real part: x = Re z = 2.316
Imaginary part: y = Im z = 0.78614099
z = 2.3158967+0.786141i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 18°45'
Polar form:
z = 2.4456891 × (cos 18°45' + i sin 18°45')
Exponential form:
z = 2.4456891 × ei 0.3272492 = 2.4456891 × ei 0.1041667 π
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 0.3272492 rad = 18.75° = 18°45' = 0.1041667π rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.3158967+0.786141i
Real part: x = Re z = 2.316
Imaginary part: y = Im z = 0.78614099
z16 = ((-5i)^(1/8))*(8^(1/3)) = 1.0817006+2.1934719i = 2.4456891 × ei 17π/48 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-5π/16) = 0.679376-1.0167581i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1+1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (0.679376-1.0167581i) * (-1+1.7320508i) = 0.67937602882697 * (-1) + 0.67937602882697 * 1.7320508076i + (-1.0167580798154i) * (-1) + (-1.0167580798154i) * 1.7320508076i = -0.67937603+1.1767138i+1.01675808i-1.76107665i2 = -0.67937603+1.1767138i+1.01675808i+1.76107665 = -0.67937603 1.761077 +i(1.1767138 + 1.016758) = 1.0817006+2.1934719ialternative steps1.2228445 × ei (-5π/16) × 2 × ei 2π/3 = 1.2228445 × 2 × ei ((-5π/16)+2π/3) = 2.4456891 × ei 17π/48 = 1.0817006+2.1934719i
The result z16
Rectangular form (standard form):
z = 1.0817006+2.1934719i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 63°45'
Polar form:
z = 2.4456891 × (cos 63°45' + i sin 63°45')
Exponential form:
z = 2.4456891 × ei 1.1126474 = 2.4456891 × ei 17π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 1.1126474 rad = 63.75° = 63°45' = 0.3541667π = 17π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 1.0817006+2.1934719i
Real part: x = Re z = 1.082
Imaginary part: y = Im z = 2.19347188
z = 1.0817006+2.1934719i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 63°45'
Polar form:
z = 2.4456891 × (cos 63°45' + i sin 63°45')
Exponential form:
z = 2.4456891 × ei 1.1126474 = 2.4456891 × ei 17π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 1.1126474 rad = 63.75° = 63°45' = 0.3541667π = 17π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 1.0817006+2.1934719i
Real part: x = Re z = 1.082
Imaginary part: y = Im z = 2.19347188
z17 = ((-5i)^(1/8))*(8^(1/3)) = -1.6125549-1.8387664i = 2.4456891 × ei (-35π/48) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei -0.1963495 = 1.2228445 × ei (-0.0625) π = 1.1993479-0.2385651i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1-1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (1.1993479-0.2385651i) * (-1-1.7320508i) = 1.19934793 * (-1) + 1.19934793 * (-1.7320508076i) + (-0.2385651361i) * (-1) + (-0.2385651361i) * (-1.7320508076i) = -1.19934793-2.07733155i+0.23856514i+0.41320694i2 = -1.19934793-2.07733155i+0.23856514i-0.41320694 = -1.19934793- 0.413207 +i(-2.07733155 + 0.238565) = -1.6125549-1.8387664ialternative steps1.2228445 × ei -0.1963495 = 1.2228445 × ei (-0.0625) π × 2 × ei (-2π/3) = 1.2228445 × 2 × ei ((-0.0625)+(-2π/3)) = 2.4456891 × ei (-35π/48) = -1.6125549-1.8387664i
The result z17
Rectangular form (standard form):
z = -1.6125549-1.8387664i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -131°15'
Polar form:
z = 2.4456891 × (cos (-131°15') + i sin (-131°15'))
Exponential form:
z = 2.4456891 × ei -2.2907446 = 2.4456891 × ei (-35π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -2.2907446 rad = -131.25° = -131°15' = -0.7291667π = -35π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -1.6125549-1.8387664i
Real part: x = Re z = -1.613
Imaginary part: y = Im z = -1.83876641
z = -1.6125549-1.8387664i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -131°15'
Polar form:
z = 2.4456891 × (cos (-131°15') + i sin (-131°15'))
Exponential form:
z = 2.4456891 × ei -2.2907446 = 2.4456891 × ei (-35π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -2.2907446 rad = -131.25° = -131°15' = -0.7291667π = -35π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -1.6125549-1.8387664i
Real part: x = Re z = -1.613
Imaginary part: y = Im z = -1.83876641
z18 = ((-5i)^(1/8))*(8^(1/3)) = 0.1599557-2.4404527i = 2.4456891 × ei (-23π/48) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 3π/16 = 1.0167581+0.679376i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1-1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (1.0167581+0.679376i) * (-1-1.7320508i) = 1.0167580798154 * (-1) + 1.0167580798154 * (-1.7320508076i) + 0.67937602882697i * (-1) + 0.67937602882697i * (-1.7320508076i) = -1.01675808-1.76107665i-0.67937603i-1.1767138i2 = -1.01675808-1.76107665i-0.67937603i+1.1767138 = -1.01675808 1.176714 +i(-1.76107665 - 0.679376) = 0.1599557-2.4404527ialternative steps1.2228445 × ei 3π/16 × 2 × ei (-2π/3) = 1.2228445 × 2 × ei (3π/16+(-2π/3)) = 2.4456891 × ei (-23π/48) = 0.1599557-2.4404527i
The result z18
Rectangular form (standard form):
z = 0.1599557-2.4404527i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -86°15'
Polar form:
z = 2.4456891 × (cos (-86°15') + i sin (-86°15'))
Exponential form:
z = 2.4456891 × ei -1.5053465 = 2.4456891 × ei (-23π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -1.5053465 rad = -86.25° = -86°15' = -0.4791667π = -23π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 0.1599557-2.4404527i
Real part: x = Re z = 0.16
Imaginary part: y = Im z = -2.44045268
z = 0.1599557-2.4404527i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -86°15'
Polar form:
z = 2.4456891 × (cos (-86°15') + i sin (-86°15'))
Exponential form:
z = 2.4456891 × ei -1.5053465 = 2.4456891 × ei (-23π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -1.5053465 rad = -86.25° = -86°15' = -0.4791667π = -23π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 0.1599557-2.4404527i
Real part: x = Re z = 0.16
Imaginary part: y = Im z = -2.44045268
z19 = ((-5i)^(1/8))*(8^(1/3)) = 1.8387664-1.6125549i = 2.4456891 × ei (-11π/48) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 7π/16 = 0.2385651+1.1993479i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1-1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (0.2385651+1.1993479i) * (-1-1.7320508i) = 0.2385651361 * (-1) + 0.2385651361 * (-1.7320508076i) + 1.19934793i * (-1) + 1.19934793i * (-1.7320508076i) = -0.23856514-0.41320694i-1.19934793i-2.07733155i2 = -0.23856514-0.41320694i-1.19934793i+2.07733155 = -0.23856514 2.077332 +i(-0.41320694 - 1.199348) = 1.8387664-1.6125549ialternative steps1.2228445 × ei 7π/16 × 2 × ei (-2π/3) = 1.2228445 × 2 × ei (7π/16+(-2π/3)) = 2.4456891 × ei (-11π/48) = 1.8387664-1.6125549i
The result z19
Rectangular form (standard form):
z = 1.8387664-1.6125549i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -41°15'
Polar form:
z = 2.4456891 × (cos (-41°15') + i sin (-41°15'))
Exponential form:
z = 2.4456891 × ei -0.7199483 = 2.4456891 × ei (-11π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -0.7199483 rad = -41.25° = -41°15' = -0.2291667π = -11π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 1.8387664-1.6125549i
Real part: x = Re z = 1.839
Imaginary part: y = Im z = -1.61255487
z = 1.8387664-1.6125549i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -41°15'
Polar form:
z = 2.4456891 × (cos (-41°15') + i sin (-41°15'))
Exponential form:
z = 2.4456891 × ei -0.7199483 = 2.4456891 × ei (-11π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -0.7199483 rad = -41.25° = -41°15' = -0.2291667π = -11π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 1.8387664-1.6125549i
Real part: x = Re z = 1.839
Imaginary part: y = Im z = -1.61255487
z20 = ((-5i)^(1/8))*(8^(1/3)) = 2.4404527+0.1599557i = 2.4456891 × ei 0.0654498 = 2.4456891 × ei 0.0208333 π Calculation steps principal root
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 11π/16 = -0.679376+1.0167581i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1-1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (-0.679376+1.0167581i) * (-1-1.7320508i) = -0.67937602882697 * (-1) + (-0.67937602882697) * (-1.7320508076i) + 1.0167580798154i * (-1) + 1.0167580798154i * (-1.7320508076i) = 0.67937603+1.1767138i-1.01675808i-1.76107665i2 = 0.67937603+1.1767138i-1.01675808i+1.76107665 = 0.67937603 1.761077 +i(1.1767138 - 1.016758) = 2.4404527+0.1599557ialternative steps1.2228445 × ei 11π/16 × 2 × ei (-2π/3) = 1.2228445 × 2 × ei (11π/16+(-2π/3)) = 2.4456891 × ei 0.0654498 = 2.4456891 × ei 0.0208333 π = 2.4404527+0.1599557i
The result z20
Rectangular form (standard form):
z = 2.4404527+0.1599557i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 3°45'
Polar form:
z = 2.4456891 × (cos 3°45' + i sin 3°45')
Exponential form:
z = 2.4456891 × ei 0.0654498 = 2.4456891 × ei 0.0208333 π
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 0.0654498 rad = 3.75° = 3°45' = 0.0208333π rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.4404527+0.1599557i
Real part: x = Re z = 2.44
Imaginary part: y = Im z = 0.15995572
z = 2.4404527+0.1599557i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 3°45'
Polar form:
z = 2.4456891 × (cos 3°45' + i sin 3°45')
Exponential form:
z = 2.4456891 × ei 0.0654498 = 2.4456891 × ei 0.0208333 π
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 0.0654498 rad = 3.75° = 3°45' = 0.0208333π rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 2.4404527+0.1599557i
Real part: x = Re z = 2.44
Imaginary part: y = Im z = 0.15995572
z21 = ((-5i)^(1/8))*(8^(1/3)) = 1.6125549+1.8387664i = 2.4456891 × ei 13π/48 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei 15π/16 = -1.1993479+0.2385651i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1-1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (-1.1993479+0.2385651i) * (-1-1.7320508i) = -1.19934793 * (-1) + (-1.19934793) * (-1.7320508076i) + 0.2385651361i * (-1) + 0.2385651361i * (-1.7320508076i) = 1.19934793+2.07733155i-0.23856514i-0.41320694i2 = 1.19934793+2.07733155i-0.23856514i+0.41320694 = 1.19934793 0.413207 +i(2.07733155 - 0.238565) = 1.6125549+1.8387664ialternative steps1.2228445 × ei 15π/16 × 2 × ei (-2π/3) = 1.2228445 × 2 × ei (15π/16+(-2π/3)) = 2.4456891 × ei 13π/48 = 1.6125549+1.8387664i
The result z21
Rectangular form (standard form):
z = 1.6125549+1.8387664i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 48°45'
Polar form:
z = 2.4456891 × (cos 48°45' + i sin 48°45')
Exponential form:
z = 2.4456891 × ei 0.850848 = 2.4456891 × ei 13π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 0.850848 rad = 48.75° = 48°45' = 0.2708333π = 13π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 1.6125549+1.8387664i
Real part: x = Re z = 1.613
Imaginary part: y = Im z = 1.83876641
z = 1.6125549+1.8387664i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 48°45'
Polar form:
z = 2.4456891 × (cos 48°45' + i sin 48°45')
Exponential form:
z = 2.4456891 × ei 0.850848 = 2.4456891 × ei 13π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 0.850848 rad = 48.75° = 48°45' = 0.2708333π = 13π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = 1.6125549+1.8387664i
Real part: x = Re z = 1.613
Imaginary part: y = Im z = 1.83876641
z22 = ((-5i)^(1/8))*(8^(1/3)) = -0.1599557+2.4404527i = 2.4456891 × ei 25π/48 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-13π/16) = -1.0167581-0.679376i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1-1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (-1.0167581-0.679376i) * (-1-1.7320508i) = -1.0167580798154 * (-1) + (-1.0167580798154) * (-1.7320508076i) + (-0.67937602882697i) * (-1) + (-0.67937602882697i) * (-1.7320508076i) = 1.01675808+1.76107665i+0.67937603i+1.1767138i2 = 1.01675808+1.76107665i+0.67937603i-1.1767138 = 1.01675808- 1.176714 +i(1.76107665 + 0.679376) = -0.1599557+2.4404527ialternative steps1.2228445 × ei (-13π/16) × 2 × ei (-2π/3) = 1.2228445 × 2 × ei ((-13π/16)+(-2π/3)) = 2.4456891 × ei 25π/48 = -0.1599557+2.4404527i
The result z22
Rectangular form (standard form):
z = -0.1599557+2.4404527i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 93°45'
Polar form:
z = 2.4456891 × (cos 93°45' + i sin 93°45')
Exponential form:
z = 2.4456891 × ei 1.6362462 = 2.4456891 × ei 25π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 1.6362462 rad = 93.75° = 93°45' = 0.5208333π = 25π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -0.1599557+2.4404527i
Real part: x = Re z = -0.16
Imaginary part: y = Im z = 2.44045268
z = -0.1599557+2.4404527i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 93°45'
Polar form:
z = 2.4456891 × (cos 93°45' + i sin 93°45')
Exponential form:
z = 2.4456891 × ei 1.6362462 = 2.4456891 × ei 25π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 1.6362462 rad = 93.75° = 93°45' = 0.5208333π = 25π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -0.1599557+2.4404527i
Real part: x = Re z = -0.16
Imaginary part: y = Im z = 2.44045268
z23 = ((-5i)^(1/8))*(8^(1/3)) = -1.8387664+1.6125549i = 2.4456891 × ei 37π/48 Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-9π/16) = -0.2385651-1.1993479i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1-1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (-0.2385651-1.1993479i) * (-1-1.7320508i) = -0.2385651361 * (-1) + (-0.2385651361) * (-1.7320508076i) + (-1.19934793i) * (-1) + (-1.19934793i) * (-1.7320508076i) = 0.23856514+0.41320694i+1.19934793i+2.07733155i2 = 0.23856514+0.41320694i+1.19934793i-2.07733155 = 0.23856514- 2.077332 +i(0.41320694 + 1.199348) = -1.8387664+1.6125549ialternative steps1.2228445 × ei (-9π/16) × 2 × ei (-2π/3) = 1.2228445 × 2 × ei ((-9π/16)+(-2π/3)) = 2.4456891 × ei 37π/48 = -1.8387664+1.6125549i
The result z23
Rectangular form (standard form):
z = -1.8387664+1.6125549i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 138°45'
Polar form:
z = 2.4456891 × (cos 138°45' + i sin 138°45')
Exponential form:
z = 2.4456891 × ei 2.4216443 = 2.4456891 × ei 37π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 2.4216443 rad = 138.75° = 138°45' = 0.7708333π = 37π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -1.8387664+1.6125549i
Real part: x = Re z = -1.839
Imaginary part: y = Im z = 1.61255487
z = -1.8387664+1.6125549i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ 138°45'
Polar form:
z = 2.4456891 × (cos 138°45' + i sin 138°45')
Exponential form:
z = 2.4456891 × ei 2.4216443 = 2.4456891 × ei 37π/48
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = 2.4216443 rad = 138.75° = 138°45' = 0.7708333π = 37π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -1.8387664+1.6125549i
Real part: x = Re z = -1.839
Imaginary part: y = Im z = 1.61255487
z24 = ((-5i)^(1/8))*(8^(1/3)) = -2.4404527-0.1599557i = 2.4456891 × ei (-47π/48) Calculation steps
- Divide: 1 / 8 = 1/1 · 1/8 = 1 · 1/1 · 8 = 1/8 = 0.125
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 8/1 is 1/8) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by eight equals one eighth. - Exponentiation: (-5i) ^ the result of step No. 1 = (-5i) ^ 0.125 = (5 × ei (-π/2))0.125 = 50.125 × ei 0.125 × (-π/2) = 1.2228445 × ei (-5π/16) = 0.679376-1.0167581i
- Divide: 1 / 3 = 1/1 · 1/3 = 1 · 1/1 · 3 = 1/3 = 0.33333333
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/1 is 1/3) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, it cannot further simplify the fraction result by canceling.
In other words, one divided by three equals one third. - Cube root: ∛8 = -1-1.7320508i
- Multiple: the result of step No. 2 * the result of step No. 4 = (0.679376-1.0167581i) * (-1-1.7320508i) = 0.67937602882697 * (-1) + 0.67937602882697 * (-1.7320508076i) + (-1.0167580798154i) * (-1) + (-1.0167580798154i) * (-1.7320508076i) = -0.67937603-1.1767138i+1.01675808i+1.76107665i2 = -0.67937603-1.1767138i+1.01675808i-1.76107665 = -0.67937603- 1.761077 +i(-1.1767138 + 1.016758) = -2.4404527-0.1599557ialternative steps1.2228445 × ei (-5π/16) × 2 × ei (-2π/3) = 1.2228445 × 2 × ei ((-5π/16)+(-2π/3)) = 2.4456891 × ei (-47π/48) = -2.4404527-0.1599557i
The result z24
Rectangular form (standard form):
z = -2.4404527-0.1599557i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -176°15'
Polar form:
z = 2.4456891 × (cos (-176°15') + i sin (-176°15'))
Exponential form:
z = 2.4456891 × ei -3.0761428 = 2.4456891 × ei (-47π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -3.0761428 rad = -176.25° = -176°15' = -0.9791667π = -47π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.4404527-0.1599557i
Real part: x = Re z = -2.44
Imaginary part: y = Im z = -0.15995572
z = -2.4404527-0.1599557i
Angle notation (phasor, module and argument):
z = 2.4456891 ∠ -176°15'
Polar form:
z = 2.4456891 × (cos (-176°15') + i sin (-176°15'))
Exponential form:
z = 2.4456891 × ei -3.0761428 = 2.4456891 × ei (-47π/48)
Polar coordinates:
r = |z| = 2.4456891 ... magnitude (modulus, absolute value)
θ = arg z = -3.0761428 rad = -176.25° = -176°15' = -0.9791667π = -47π/48 rad ... angle (argument or phase)
Cartesian coordinates:
Cartesian form of imaginary number: z = -2.4404527-0.1599557i
Real part: x = Re z = -2.44
Imaginary part: y = Im z = -0.15995572
This calculator performs all operations on complex numbers and evaluates expressions within the set of complex numbers.
As an imaginary unit, use i or j (in electrical engineering), which satisfies the basic equation i2 = −1 or j2 = −1. The calculator also converts a complex number into angle notation (phasor notation), exponential, or polar coordinates (magnitude and angle). Enter expression with complex numbers like 5*(1+i)(-2-5i)^2
Complex numbers in the angle notation or phasor (polar coordinates r, θ) may you write as rLθ where r is magnitude/amplitude/radius, and θ is the angle (phase) in degrees, for example, 5L65 which is the same as 5*cis(65°).
Example of multiplication of two imaginary numbers in the angle/polar/phasor notation: 10L45 * 3L90.
For use in education (for example, calculations of alternating currents at high school), you need a quick and precise complex number calculator.
Example of multiplication of two imaginary numbers in the angle/polar/phasor notation: 10L45 * 3L90.
For use in education (for example, calculations of alternating currents at high school), you need a quick and precise complex number calculator.
Basic operations with complex numbers
We hope that working with the complex number is quite easy because you can work with imaginary unit i as a variable. And use the definition i2 = -1 to simplify complex expressions. Many operations are the same as operations with two-dimensional vectors.Addition
It is very simple: add up the real parts (without i) and add up the imaginary parts (with i):This is equal to use rule: (a+bi)+(c+di) = (a+c) + (b+d)i
(1+i) + (6-5i) = 7-4i
12 + 6-5i = 18-5i
(10-5i) + (-5+5i) = 5
Subtraction
Again it is very simple: subtract the real parts and subtract the imaginary parts (with i):This is equal to use rule: (a+bi)+(c+di) = (a-c) + (b-d)i
(1+i) - (3-5i) = -2+6i
-1/2 - (6-5i) = -6.5+5i
(10-5i) - (-5+5i) = 15-10i
Multiplication
To multiply two complex numbers, use distributive law, avoid binomials, and apply i2 = -1.This is equal to use rule: (a+bi)(c+di) = (ac-bd) + (ad+bc)i
(1+i) (3+5i) = 1*3+1*5i+i*3+i*5i = 3+5i+3i-5 = -2+8i
-1/2 * (6-5i) = -3+2.5i
(10-5i) * (-5+5i) = -25+75i
Division
The division of two complex numbers can be accomplished by multiplying the numerator and denominator by the denominator's complex conjugate. This approach avoids imaginary unit i from the denominator. If the denominator is c+di, to make it without i (or make it real), multiply with conjugate c-di:(c+di)(c-di) = c2+d2
c+dia+bi=(c+di)(c−di)(a+bi)(c−di)=c2+d2ac+bd+i(bc−ad)=c2+d2ac+bd+c2+d2bc−adi
(10-5i) / (1+i) = 2.5-7.5i
-3 / (2-i) = -1.2-0.6i
6i / (4+3i) = 0.72+0.96i
Absolute value or modulus
The absolute value or modulus is the distance of the image of a complex number from the origin in the plane. The calculator uses the Pythagorean theorem to find this distance. Very simple, see examples: |3+4i| = 5|1-i| = 1.4142136
|6i| = 6
abs(2+5i) = 5.3851648
Square root
The square root of a complex number (a+bi) is z, if z2 = (a+bi). Here ends simplicity. Because of the fundamental theorem of algebra, you will always have two different square roots for a given number. If you want to find out the possible values, the easiest way is to use De Moivre's formula. Our calculator is on edge because the square root is not a well-defined function on a complex number. We calculate all complex roots from any number - even in expressions:sqrt(9i) = 2.1213203+2.1213203i
sqrt(10-6i) = 3.2910412-0.9115656i
pow(-32,1/5)/5 = -0.4
pow(1+2i,1/3)*sqrt(4) = 2.439233+0.9434225i
pow(-5i,1/8)*pow(8,1/3) = 2.3986959-0.4771303i
Square, power, complex exponentiation
Our calculator can power any complex number to an integer (positive, negative), real, or even complex number. In other words, we calculate 'complex number to a complex power' or 'complex number raised to a power'...Famous example:
ii=e−π/2
i^2 = -1i^61 = i
(6-2i)^6 = -22528-59904i
(6-i)^4.5 = 2486.1377428-2284.5557378i
(6-5i)^(-3+32i) = 2929449.0399425-9022199.5826224i
i^i = 0.2078795764
pow(1+i,3) = -2+2i
Functions
- sqrt
- Square Root of a value or expression.
- sin
- the sine of a value or expression. Autodetect radians/degrees.
- cos
- the cosine of a value or expression. Autodetect radians/degrees.
- tan
- tangent of a value or expression. Autodetect radians/degrees.
- exp
- e (the Euler Constant) raised to the power of a value or expression
- pow
- Power one complex number to another integer/real/complex number
- ln
- The natural logarithm of a value or expression
- log
- The base-10 logarithm of a value or expression
- abs or |1+i|
- The absolute value of a value or expression
- phase
- Phase (angle) of a complex number
- cis
- is less known notation: cis(x) = cos(x)+ i sin(x); example: cis (pi/2) + 3 = 3+i
- conj
- the conjugate of a complex number - example: conj(4i+5) = 5-4i
Examples:
• cube root: cuberoot(1 - 27i)• roots of Complex Numbers: pow(1 + i,1/7)
• phase, complex number angle: phase(1 + i)
• cis form complex numbers: 5 * cis(45°)
• The polar form of complex numbers: 10L60
• complex conjugate calculator: conj(4 + 5i)
• equation with complex numbers: (z + i/2 )/(1 - i) = 4z + 5i
• system of equations with imaginary numbers: x - y = 4 + 6i; 3ix + 7y=x + iy
• De Moivre's theorem - equation: z ^ 4=1
• multiplication of three complex numbers: (1 + 3i)(3 + 4i)(−5 + 3i)
• Find the product of 3-4i and its conjugate.: (3 - 4i) * conj(3 - 4i)
• operations with complex numbers: (3 - i) ^ 3
Complex numbers in word problems:
- Suppose 5
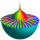 Suppose z5=2+3i and z6=6+9i are complex numbers and 3 z5 + 7 z6= m+in. What is the value of m and n?
Suppose z5=2+3i and z6=6+9i are complex numbers and 3 z5 + 7 z6= m+in. What is the value of m and n? - The expression 2
 The expression (3+i)(1+2i) can be written in the form a+bi, where a and b are integers. What are the values of a and b?
The expression (3+i)(1+2i) can be written in the form a+bi, where a and b are integers. What are the values of a and b? - Real and imaginary parts
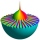 Let z1=x1+y1i and z2=x2+y2i Find: a = Im (z1z2) b = Re (z1/z2)
Let z1=x1+y1i and z2=x2+y2i Find: a = Im (z1z2) b = Re (z1/z2) - Cis notation
 Evaluate the multiplication of two complex numbers in cis notation: (6 cis 120°)(4 cis 30°) Write the result in cis and Re-Im notation.
Evaluate the multiplication of two complex numbers in cis notation: (6 cis 120°)(4 cis 30°) Write the result in cis and Re-Im notation.
- Simplify complex expr
 Perform the indicated operations and write the results in the form of a + bi: (2 + 3i)³ (ii) (1 + i)⁴
Perform the indicated operations and write the results in the form of a + bi: (2 + 3i)³ (ii) (1 + i)⁴ - Linear combination of complex
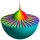 If z1=5+3i and z2=4-2i, write the following in the form a+bi a) 4z1+6z2 b) z1*z2
If z1=5+3i and z2=4-2i, write the following in the form a+bi a) 4z1+6z2 b) z1*z2 - Complex expr with fractions
 Find 1½ of 16 ÷2⅓+(2¼ of ⅑). Use the correct order of operations. The order is PEMDAS: Parentheses, Exponents, Multiplication, Division (from left to right), addition, and Subtraction (from left to right).
Find 1½ of 16 ÷2⅓+(2¼ of ⅑). Use the correct order of operations. The order is PEMDAS: Parentheses, Exponents, Multiplication, Division (from left to right), addition, and Subtraction (from left to right).
more math problems »
