Příklady na zlomky - strana 109 z 126
Zlomek je matematický výraz, který představuje část celku. Píše se jako dvě čísla oddělená čarou nebo lomítkem (zlomkovou čarou), přičemž číslo nahoře se nazývá čtenář a číslo v dolní části se nazývá jmenovatel. Čtenář představuje počet částí celku, které se zvažují, a jmenovatel představuje celkový počet částí, na které je celek rozdělen. Například, pokud máte pizzu a chcete ji sdílet se 3 lidmi, každý obdrží 1/3 pizzy. Čtenář (1) představuje počet částí, které obdrží každá osoba, a jmenovatel (3) představuje celkový počet částí, na které je pizza rozdělena. Zlomky lze zjednodušit, porovnávat, sčítat, odečítat, násobit a dělit stejně jako jakákoli jiná čísla.Počet nalezených příkladů: 2517
- Huby
Dědeček nasbíral čerstvé houby. Pětina byla červivé, ty vyhodil, ostatní usušil. Získal tak 720 gramů sušených hub. Kolik kilogramů nasbíral dědeček, jestliže sušením houby ztratily 75% své hmotnosti? - V terénu - věta SSU
V terénu byla měřena vzdálenost bodů P a Q rovná 356 m. Úsečka PQ je vidět od pozorovatele pod zorným úhlem 107°22'. Vzdálenost pozorovatele od místa P je 271 m. Urči zorný úhel, pod kterým je vidět místo P a pozorovatele. - Automobil 21
Automobil projel první třetinu dráhy s stálou rychlostí o velikosti v1, další dvě třetiny dráhy stálou rychlostí o v2 72km/h, průměrná rychlost vp byla 36km/h. Urči v1. - Fahrenheita(F) 19813
Při převodu stupňů Celsia(C) na stupně Fahrenheita(F) se používá vztah: F = C . 9/5 + 32. Kolik stupňů Celsia mají ve městě New York, pokud jim teploměr ukazuje 23 stupňů Fahrenheita?
- Trojúhelníku 31991
Vypočítejte objem a povrch hranolu, jehož výška je 16cm a podstava má tvar pravoúhlého trojúhelníku s odvěsnami 5cm a 12cm a přeponou 13cm. - Trojúhelníku 7474
Vypočítejte největší úhel trojúhelníku, jehož strany jsou 5,2 cm, 3,6 cm a 2,1 cm - Rovnostranny kužel
Do nádoby tvaru rovnostranného kužele, jehož podstava má poloměr r = 6 cm nalijeme tolik vody, že se naplní jedna třetina objemu kužele. Do jaké výšky bude sahat voda, pokud kužel obrátíme dnem vzhůru? - Vypočítej úseč
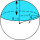Vypočítejte objem kulového úseče a obsah kulového vrchlíku, pokud r = 5 cm (poloměr koule), ρ = 4 cm (poloměr kružnice úseče). - Hranol RRPT
Vypočítejte objem a povrch hranolu o výšce 120mm, jehož podstavce je rovnoramenný trojúhelník s odvěsnou dlouhou 5cm.
- Obdélníkovým 62964
Přístřešek na auto je třeba přikrýt valbovou střechou s obdélníkovým průřezem 8 m x 5 m. Všechny střešní plochy mají stejný sklon 30°. Určete cenu a hmotnost střechy, pokud 1 m² stojí 270 € a váží 43 kg. - Aritmetickou 76704
Najděte všechny pravoúhlé trojúhelníky, jejichž délky stran tvoří aritmetickou posloupnost. - Vypočítej 40981
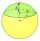Průnik roviny vzdálené od středu koule 2 cm a této koule je kruh, jehož poloměr je 6cm. Vypočítej povrch a objem koule. - Pravděpodobnost 72834
Pravděpodobnost, že životnost žárovky bude více než 682 hodin, je 0,9788. Pravděpodobnost, že žárovka bude mít životnost více než 703 hodin, je 0,0051. Najděte pravděpodobnost, že žárovka vydrží více než 648 hodin. - Trojúhelníku 17003
Jaký objem má otvor vyvrtaný vrtákem tvaru pravoúhlého trojúhelníku který se otáčí kolem delší odvěsny? Odvěsny trojúhelníku mají délku 10 cm a 3 cm?
- Prostřednictvím 74144
Hmota o hmotnosti 50 kg sedí na povrchu bez tření. Neznámá konstantní síla tlačí hmotu po dobu 2 sekund, dokud hmota nedosáhne rychlosti 3 m/s. Jaká je hodnota neznámé síly? b) dokažte, že impuls a hybnost budou mít prostřednictvím vašich řešení stejnou h - Výška 9
Vypočítej výšku na stranu d trojúhelníků BCD: d =0,4 m a S= 10,04 dm2 - Pravidelný 11
Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu - Výrobce 4
Výrobce auta uvádí, že auto spotřebuje průměrně 6,8l benzinu na 100km. Kolik litrů benzinu spotřebuje na cestu dlouhou 348 km? - Zámecká věž
Zámecká věž má střechu kuželu s průměrem 10 metrů a výškou 8 metrů. Vypočítejte, kolik m² krytiny je třeba na její pokrytí, uvažujeme-li navíc jednu třetinu na překrytî.
Osový řez kužele je rovnostranný trojúhelník se stranou 12cm. Výpočet povrchu a objemu.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
