Triangle + similarity of triangles - practice problems - page 7 of 8
Number of problems found: 147
- The straight
The straight path rises by 72 cm every 3 m of its length. How many meters will it climb to 350 m? - Sun rays
If the sun's rays are at an angle of 60°, then the famous Great Pyramid of Egypt (which is now 137.3 meters high) has a 79.3 m long shadow. Calculate the current height of the neighboring Chephren pyramid, whose shadow is measured at the same time at 78.8 - Trapezoid IV
In a trapezoid ABCD (AB||CD) is |AB| = 15cm |CD| = 7 cm, |AC| = 12 cm, AC is perpendicular to BC. What area has a trapezoid ABCD? - Sides of the triangle
The sides of the triangle ABC have a length of 4 cm, 5 cm, and 7 cm. Construct triangle A'B'C', similar to triangle ABC, which has a circumference of 12 cm.
- Circumscribed 83357
Calculate the radius of the circle of the circumscribed triangle, which has side dimensions of 8, 10, and 14 cm. - An observer
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower? - Climb
The road sign that informs the climb is 10.3%—the car drives 10 km along this road. What is the height difference that the car went? - Rectangular trapezoid
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - MO Z9–I–2 - 2017
VO is a longer base in the VODY trapezoid, and the diagonal intersection K divides the VD line in a 3:2 ratio. The area of the KOV triangle is 13.5 cm². Find the area of the entire trapezoid.
- Divide an isosceles triangle
How can an isosceles triangle be divided into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)? - Isosceles trapezoid
In an isosceles trapezoid KLMN, the intersection of the diagonals is marked by the letter S. Calculate the area of the trapezoid if /KS/: /SM/ = 2:1 and a triangle KSN is 14 cm². - Diagonals at right angle
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - Right circular cone
The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone. - Hexagon
There is a regular hexagon ABCDEF. If the area of the triangle ABC is 10, what is the area of the hexagon ABCDEF? I do not know how to solve it simply....
- Quadrilateral 11241
The regular quadrilateral pyramid has a height of 40 cm and a base side of 21 cm. Cut the needle at half the height. How much will both parts have? - Pentagon
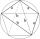The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Secret treasure
Scouts have a tent in the shape of a regular quadrilateral pyramid with a side of the base of 4 m and a height of 3 m. Find the container's radius r (and height h) so that they can hide the largest possible treasure. - Hexagon cut pyramid
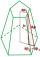Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm. - Distance of points
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S.
Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
