Right triangle practice problems - page 16 of 84
Number of problems found: 1671
- Parametrically 6400
Find the angle of the line, which is determined parametrically x = 5 + t y = 1 + 3t z = -2t t belongs to R and the plane, which is determined by the general equation 2x-y + 3z-4 = 0. - Airplane navigation
An airplane leaves an airport and flies west 120 miles and then 150 miles in the direction S 32.12°W. How far is the plane from the airport (round to the nearest mile)? - Identical 8831
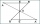In triangle ABC, point P lies closer to point A in the third of line AB, point R is closer to point P in the third of line P, and point Q lies on line BC, so the angles P CB and RQB are identical. Determine the ratio of the area of the triangles ABC and P - Luiza
Luiza delivers newspapers in her neighborhood. If you plot the points (-1, 1), (4, 1), (4, -2), and (-1, -2), you will create a representation of the route she takes in miles. How many miles does her route cover?
- Display case
Place a glass shelf at the height of 1m from the bottom of the display case in the cabinet. How long platter will we place at this height? The display case is a rectangular triangle with 2 m and 2.5 m legs. - Triangle KLB
It is given an equilateral triangle ABC. From point L, the midpoint of the side BC of the triangle, it is drawn perpendicular to the side AB. The intersection of the perpendicular and the side AB is point K. How many percent of the area of the triangle AB - Isosceles 7661
The area of the isosceles triangle is 8 cm2, and its arm's length is 4 cm. Calculate the sizes of its interior angles. - Squares above sides
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2:1 ratio. The AC side is longer than the BC side. Calcu - Acute triangle
In the acute triangle KLM, V is the intersection of its heights, and X is the heel of height to the side KL. The axis of the angle XVL is parallel to the side LM, and the angle MKL is 70°. What size are the KLM and KML angles?
- Mr. Bradshaw
Mr. Bradshaw is leaning a ladder against the side of his house to repair the roof. The top of the ladder reaches the roof, which is 5 meters high. The ladder's base is 1 meter away from the house, where Mr. Bradshaw's son is holding it steady. How long is - Perpendicular 81837
Two neighboring cottagers have cottages under the forest by the stream. They decided to build a bridge over the stream at a place far from the two huts. The distance between the cottages is 230 m; one cottage is 120 m from the stream, and the other is 85 - Shadow 73354
How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long? - A boy
A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff. - Equilateral 7962
After a long dinner, inside a lounge in the shape of a square ABCD, a drunken shopper E lies in such a way that the triangle DEC is equilateral. Spy F lies on the edge of BC, with |EB|=|EF|. What is the size of the angle CEF?
- Determine 70834
At the same time, a vertical 2-meter pole casts a shadow of 0.85 meters. At the same time, a chimney of unknown height casts a 45m long shadow. Determine the height of the chimney. - Shadows At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
- Three points
Three points, K (-3; 2), L (-1; 4), and M (3, -4), are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write - Mast shadow
The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - Boat
A force of 300 kg (3000 N) is required to pull a boat up a ramp inclined at 14° with horizontal. How much does the boat weigh?
Draw an equilateral triangle ABC with a side of 8.5 cm. Assemble all the mines and measure them. What is the difference between the longest and the shortest of them?Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
