Reason + multiplication principle - practice problems - page 3 of 12
Number of problems found: 228
- In an
In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square. - A bag 2
A bag contains seven green and eight red jellybeans. How many ways can five jellybeans be withdrawn from the bag so that the number of green ones withdrawn will be less than 4? - Calculation 73364
From the number 5,4,0,7,8, create three-digit numbers, so they do not repeat and solve the problem by calculation. - Probability 73054
We roll six dice. What is the probability that: a) a six falls twice b) six falls four times
- Between 72924
How many ways do we know to select three cards from a deck of seven cards so that there are two red and one green between them? - Probability 72324
When entering the PIN code, we used the digits 2, 3, 4, 5, and 7 only once. What is the probability that someone will guess our PIN code on the first try? - Groups 72194
I have eight groups. How could they place first, second, and third? - Identical 71234
How many ways can you divide two identical apples and: a) 3, b) 4, c) 5 identical pears between Janka and Mařenka? - Distinguish 71184
We randomly choose a family with three children. We distinguish between gender and age. Determine the probability that: a) the youngest girl will be among the children b) all children will be of the same sex
- Probability 71174 Find the probability that one will fall at least once in three rolls.
- Two-digit 71134 How many natural two-digit numbers can we form from the digits 0, 1, 2, and 3 if we cannot repeat the digits in these numbers?
- Distribute 70244
We have to distribute the keys to the safe among four people so that no two of them can open the safe but in such a way that any three can open the safe. How many minimum keys do we need? How to divide them? How many minimum locks must be on the safe? All - Together 70124
Twins Ela and Nela came to the cinema together with their friend Hela. Only the first 10 seats in the third row are free. How many ways can they be seated if the twins want to sit next to each other, with Nela always to Ela's left and Hel right next to on - Differently 69514
Gabika wants to wear pants, a blouse, a skirt, and a T-shirt to the party. She has two pairs of pants, 3 blouses, 3 skirts, and 4 T-shirts to choose from. How many parties can she attend if everyone wants to go dressed differently?
- Equipment 69464 Miša is buying skater equipment. He chooses one of 2 helmets, one of three gloves, one of four knee pads, and one of two elbow pads. How many options does it have for buying equipment?
- Wallpapers 69424 Lucia's mobile phone offers a choice of 10 ringtones, seven tones when receiving an SMS, and 15 wallpapers in the background of the display. How many ways can Lucia set up her mobile?
- Different 68064
Anna painted eggs for art. She had five colors for her eggs. He wants to put three of them on each. How many different colored eggs could she paint? (It's just the colors, not the shapes on them. ) - Triples 67394
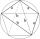How many triples of sounds can be created from sounds f, o, u, r? You solve using a tree diagram. - Competition 67314
The coach must choose two students from Sam, Jura, Emma, Dan, and Nika to go to the competition. He knows them well and knows that Samo will only go with Jura or Ema, and Dano will not go with Ema. How many pairs does the trainer have to choose from?
Without listing all the possibilities, calculate how many different pairs can be made A) of 12 pupils who want to go down a water slide on a two-seater inflatable in the water park. B) of 15 pupils who want to ride toy cars in the amusement park.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
