Pyramid practice problems - page 12 of 13
Number of problems found: 256
- Quadrilateral 46431
Calculate the volume V and the surface S of a regular quadrilateral pyramid, the base edge and height of which are the same size as the edge of a cube with a volume V1 = 27m3 - Tower
Charles built a tower of cubes with an edge 2 cm long. In the lowest layer, there were six cubes (in one row) in six rows. In each subsequent layer, always one cube and one row less. What volume in cm³ did the whole tower have? - Calculate 25391
The base of the prism is a square with a side of 10 cm. Its height is 20 cm. Calculate the height of a pyramid with a square base of 10 cm, which has four times the prism's volume. - Calculate 25321 Calculate the body's volume, consisting of a prism and a pyramid with the same square base with an edge of 8 cm. The prism is 20 cm high, and the pyramid is 15 cm.
- Pyramid 7903
How does the volume of a pyramid change if we triple its height? - Consumption 4259
What is the consumption of fabric per tent: Length 250, width 180, the height of triangle 120, sides 150 (all cm). What is the volume of air in the tent? - Rotating cone
How does the volume of the rotating cone change if: a) double the radius of the base b) We reduce the height three times c) Reduce the radius of the base five times - Consumption 15663
The cone-shaped sheet metal roof has a base diameter of 80 cm and a height of 60 cm. If 1 kg of paint is consumed per 6 m² of sheet metal, calculate the paint consumption for painting this roof. - Calculate 83248
The cube ABCDEFGH has an edge of length 3 cm. Calculate the volume of the pyramid ABCDH.
- From plasticine
Michael modeled from plasticine a 15 cm high pyramid with a rectangular base, with the sides of the base a = 12 cm and b = 8 cm. From this pyramid, Janka modeled a rotating cone with a base diameter of 10 cm. How tall was Janka's cone? - Pit
The pit is 0.8 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.6 l of green paint. How many liters of paint are n - Cone
The rotating cone volume is 9.42 cm3, with a height of 10 cm. What angle is between the side of the cone and its base? - Tetrahedron 82497
The sum of the lengths of all the edges of the regular tetrahedron ABCD is 48 cm. How many cm is the segment XY if you know that X is AB's midpoint and Y is CD's midpoint? - Surface 64744
The cone is 12 cm high, and the radius of the figure is 9 cm. Find out its surface.
- Runcated pyramid teapot
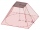The 35 cm high teapot has the shape of a truncated pyramid with the length of the edge of the lower square base a=50 cm and the edges of the rectangular base b: 20 cm and c: 30 cm. How many liters of water will fit in the teapot? - Truncated 43851
The pit is a regular truncated 4-sided pyramid, with 14 m and 10 m base edges and a depth of 6m. Calculate how much m³ of soil was removed when we dug this pit. - Flowerbed
The flowerbed has the shape of a truncated pyramid. The bottom edge of the base a = 10 m, and the upper base b = 9 m. The deviation angle between the edge and the base is alpha = 45°. What volume is needed to make this flowerbed? How many plants can be pl - Digging a pit
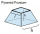The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit. - Hexagon cut pyramid
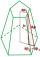Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm.
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =?Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
