Length + similarity of triangles - practice problems - page 2 of 4
Number of problems found: 63
- The straight
The straight path rises by 72 cm every 3 m of its length. How many meters will it climb to 350 m? - Poplar shadow
The nine-meter poplar casts a shadow 16.2 m long. How long does a shadow cast by Peter at the same time if it is 1.4 m high? - Chimney and tree Calculate the height of the factory chimney, which casts a shadow of 6.5 m long in the afternoon. At the same time, a 6 m high tree standing near it casts a shadow 25 dm long.
- Similar triangles
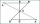Triangle A'B'C 'is similar to triangle ABC, whose sides are 5 cm, 8 cm, and 7 cm long. What is the length of the sides of the triangle A'B'C' if its circumference is 80 cm?
- Similar triangles
The triangles ABC and XYZ are similar. Find the unknown lengths of the sides of the triangles. a) a = 5 cm b = 8 cm x = 7.5 cm z = 9 cm b) a = 9 cm c = 12 cm y = 10 cm z = 8 cm c) b = 4 cm c = 8 cm x = 4.5 cm z = 6 cm - Triangle 28611 The land has a triangle shape with sides of 300m, 200m, and 245m. Draw it on a scale of 1:5,000.
- Similarity coefficient
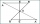In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other. - Similarity 26441
How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity. - Cutting cone
A cone with a base radius of 10 cm and a height of 12 cm is given. At what height above the base should we divide it by a section parallel to the base so that the volumes of the two resulting bodies are the same? Express the result in cm.
- Approximately 25381
The observer sees the tops of two trees at the same angle a. It is 9 m from one tree and 21 m from the other. The trees stand on a level. How tall is the second tree if the height of the first is 6 m? Remember that the eyes of a standing person are approx - The triangles
Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5 - Lookout tower
Calculate the height of a lookout tower forming a shadow of 36 m if a column 2.5 m high has a shadow of 1.5 m simultaneously. - Similarity of two triangles
The KLM triangle has a side length of k = 6.3cm, l = 8.1cm, m = 11.1cm. The triangle XYZ has a side length of x = 8.4cm, y = 10.8cm, z = 14.8cm. Are triangle KLM and XYZ similar? (write 0. If not, if yes, find and write the coefficient of a similarity) - Two chords
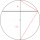Calculate the length of chord AB and perpendicular chord BC to the circle if AB is 4 cm from the circle's center and BC 8 cm from the center.
- The chimney
The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney. - Lighthouse
Marcel (point J) lies in the grass and sees the top of the tent (point T) and, behind it, the top of the lighthouse (P). | TT '| = 1.2m, | PP '| = 36m, | JT '| = 5m. Marcel lies 15 meters away from the sea (M). Calculate the lighthouse distance from the s - Trapezium diagonals
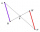It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Diagonals at right angle
In the trapezoid ABCD, this is given: AB=12cm CD=4cm And diagonals crossed under a right angle. What is the area of this trapezoid ABCD? - Mast shadow
The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines.
A man 1.65 m tall casts a shadow of 1.25 m. How tall is the tree whose shadow is in debt 2.58 m?Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
