The inscribed angle theorem of triangle problems - page 2 of 3
Number of problems found: 48
- Calculate 9701
In the triangle, the side length AB = 6 cm, the height per side c = 5 cm, and the angle BCA = 35°. Calculate sides a b. - Quadrilateral 8405
Calculate the magnitude of the largest inner angle and the deviation of the diagonals in the quadrilateral, whose vertices correspond to points 1, 5, 8, and 12 on the dial. - Isosceles 7566
A right isosceles triangle is inscribed in the circle with r = 8 cm. Find triangle area S. How much percent does the triangle occupy the area of the circle? - Spectators 7562
The theater has the shape of a semicircle, and the podium is the diameter of a semicircle. Spectators K, L, M, N, and O, sit around the perimeter. Who sees the podium at the greatest angle?
- RT - inscribed circle
In a rectangular triangle with sides lengths> a = 30cm and b = 12.5cm, the right angle is at vertex C. Calculate the radius of the inscribed circle. - Conditions 7186
Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Nonagon
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm. - Triangle - many properties
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - Inscribed circle
Calculate the magnitude of the BAC angle in triangle ABC if it is three times less than the angle BOC, where O is the center of the circle inscribed in triangle ABC.
- 30-gon
The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area. - Circular segment
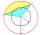Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Diagonals
Draw a square ABCD whose diagonals have a length of 6 cm. - Pentagon
Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm. - Regular n-gon
Which regular polygon has a radius of circumscribed circle r = 10 cm and the radius of inscribed circle p = 9.962 cm?
- Intersection 3383
A regular 15-angle is given. A triangle is formed if we connect points 3 and 7, 13 and 10. The vertices are 3 and 13, and the lines' intersections are 3.7 and 13.10. We are to determine the angle size formed by sides 3.7 and 13.10. These numbers indicate - Inscribed circle
XYZ is a right triangle with a right angle at the vertex X and an inscribed circle with a radius of 5 cm. Find the area of the triangle XYZ if XZ = 14 cm. - 6 regular polygon
A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon. - Complete construction
Construct triangle ABC if hypotenuse c = 7 cm and angle ABC = 30 degrees. / Use Thales' theorem - circle /. Measure and write down the length of the legs. - Diagonal in rectangle
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts.
Within a regular pentagon ABCDE point, P is such that the triangle is equilateral ABP. How big is the angle BCP? Make a sketch.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
