The inscribed angle theorem of right triangle problems
Number of problems found: 25
- Angle over circle
In the figure, O is the center of the circle and AB is tangent at B. If angle OAB is 28 degrees find angle AOB. Figure is not scaled. - Subtended 83194
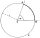A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Triangle 80994
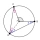In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify. - Three
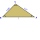Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
- Hexagonal pyramid
Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. - Calculate 9701
In the triangle, the side length AB = 6 cm, the height per side c = 5 cm, and the angle BCA = 35°. Calculate sides a b. - Isosceles 7566
A right isosceles triangle is inscribed in the circle with r = 8 cm. Find triangle area S. How much percent does the triangle occupy the area of the circle? - Spectators 7562
The theater has the shape of a semicircle, and the podium is the diameter of a semicircle. Spectators K, L, M, N, and O, sit around the perimeter. Who sees the podium at the greatest angle? - RT - inscribed circle
In a rectangular triangle with sides lengths> a = 30cm and b = 12.5cm, the right angle is at vertex C. Calculate the radius of the inscribed circle.
- Conditions 7186
Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Nonagon
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm. - Triangle - many properties
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - 30-gon
The radius of the inscribed circle is 15cm at a regular 30-gon. Find the side length a, circle radius R, circumference, and area. - Circular segment
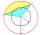Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
- Diagonals
Draw a square ABCD whose diagonals have a length of 6 cm. - Pentagon
Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm. - Regular n-gon
Which regular polygon has a radius of circumscribed circle r = 10 cm and the radius of inscribed circle p = 9.962 cm? - Inscribed circle
XYZ is a right triangle with a right angle at the vertex X and an inscribed circle with a radius of 5 cm. Find the area of the triangle XYZ if XZ = 14 cm. - 6 regular polygon
A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon.
Construct triangle ABC if hypotenuse c = 7 cm and angle ABC = 30 degrees. / Use Thales' theorem - circle /. Measure and write down the length of the legs.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
