Division + Mathematical Olympiad - practice problems
Number of problems found: 18
- Positive integer integral
How many different sets of a positive integer in the form (x, y, z) satisfy the equation xyz=1400? - Mr. Product
The product of ages of all of Mr. Product's children is 1408. The age of the youngest child is equal to half the age of the oldest child. How many children does Mr. Product have, and how old are they? - Coloured numbers
Mussel wrote four different natural numbers with colored markers: red, blue, green, and yellow. When the red number is divided by blue, it gets the green number is an incomplete proportion, and yellow represents the remainder after this division. When it - Twos
Vojta started writing the number this year, 2019202020192020, into the workbook. And so he kept going. When he wrote 2020 digits, he no longer enjoyed it. How many twos did he write?
- Sufficient 9391
In Kocourkov, they use coins with only two values expressed in Kocourkov crowns by positive integers. With a sufficient number of such coins, it is possible to pay any integer amount greater than 53 cats’ crowns accurately and without return. However, we - Solutions 8481
For which integers x is the ratio (x + 11) / (x + 7) an integer? Find all solutions. - Restriction 7442
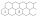The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top - Three-digit number
Find all three-digit numbers n with three different non-zero digits divisible by the sum of all three two-digit numbers we get when we delete one digit in the original number. - Definitely 7179
Ivan and Mirka shared pears in the mission. Ivan always takes two pears, and Mirka takes half of what remains in the mission. Thus, Ivan, Mirka, Ivan, Mirka, and finally Ivan, who took the last two pears, took them away. Definitely. Who had more pears, in
- MO Z8–I–6 2018
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Shopkeeper 4433
The seller of Christmas trees sold spruces for 220 CZK, pines for 250 CZK, and hemlocks for 330 CZK. In the morning he had an equal number of spruces, hemlocks, and pines. In the evening, he had sold all the trees and received a total of 36,000 CZK for th - Four families
Four families were on a joint trip. The first family had three siblings: Alica, Betka, and Cyril. In the second family were four siblings: David, Erik, Filip, and Gabika. In the third family, there were two siblings, Hugo and Iveta. Three siblings in the - Centipede 4257
Centipede Mirka consists of a head and several articles. Each pair has one pair of legs. When it got cold, she decided to get dressed. Therefore, she put a sock on her left foot from the end of the third article and then in every other third article. Simi - Christmas trees
The salesman sold Christmas trees: spruce for € 22, pine for € 25, and fir for € 33. In the morning, he had the same number of spruce, fir, and pine. In the evening, he had all the trees sold for € 3,600. How many trees does the day salesman sell?
- Fluid
We have vessels containing 7 liters, 5 liters, and 2 liters. The largest container is filled with fluid, and the others are empty. Can you only get 5 liters and two 1 liter of fluid by pouring? How much pouring is needed? - Soup
On Monday, we cooked 25 pots and ten boilers of soup. On Tuesday, we cooked 15 pots and 13 boilers. On Wednesday, we cooked 20 pots, and on Thursday, we cooked 30 boilers. The same amount of soup was cooked on Monday and Tuesday. How many times is more so - Meadow
On the meadow, there are horses, cows, and sheep grazing together with less than 200. If cows were 45 times more, horses 60 times more, and sheep 35 times more than there are now, their numbers would equal. How many horses, cows, and sheep are in the mead - Wipes
The mummy wiped out the square wipes, and the veil was next to each other on the cord stretched out between the two trees. She used a cord of 7.5 meters in length, requiring about 8 dm on each side of the trunk. All wipes are 45 cm wide. The mummy leaves
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
