Arccosine - practice problems - page 2 of 3
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 54
- Angle of the body diagonals
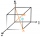Using the vector dot product calculate the angle of the body diagonals of the cube. - The aspect ratio
The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle. - Circular railway
The railway connects points A, B, and C in a circular arc, whose distances are | AB | = 30 km, AC = 95 km, and BC | = 70 km. How long will the track be from A to C? - Roof angle
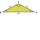The house's roof has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make?
- Isosceles triangle 8
If the rate of the sides of an isosceles triangle is 7:6:7, find the base angle correct to the nearest degree. - Calculate 2
Calculate the largest angle of the triangle whose sides are 5.2cm, 3.6cm, and 2.1cm - Substitution method
Solve a goniometric equation: sin4 θ - 1/cos² θ=cos² θ - 2 - Perpendicular direction
A speedboat moves relative to the water at a constant speed of 13 m/s. The speed of the water current in the river is 5 m/s a) At what angle concerning the water current must the boat sail to keep moving perpendicular to the banks of the river? b) At what - Right triangle eq2
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
- Parametrically 6400
Find the angle of the line, which is determined parametrically x = 5 + t y = 1 + 3t z = -2t t belongs to R and the plane, which is determined by the general equation 2x-y + 3z-4 = 0. - Largest angle of the triangle
Calculate the largest angle of the triangle whose sides have the sizes: 2a, 3/2a, 3a - Horizontal watertank
We have a horizontal tank shaped like a rainwater cylinder, 3.45 m long and 1.7 m wide. Calculate how many liters of water is in first centimeters. - Toboggan 5710
The length of the toboggan run is 60 m, and the height is 8 m. The boy pulls a sled weighing 15 kg. How hard does the boy pull the sled uphill? - Cylinder horizontally
The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the cylinder's axis. How many hectoliters of water is in the cylinder?
- Angle of deviation
The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane. - Angles by cosine law
Calculate the size of the angles of the triangle ABC if it is given by: a = 3 cm; b = 5 cm; c = 7 cm (use the sine and cosine theorem). - Four sides of trapezoid
In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles. - Isosceles 4741
The arm is five times longer than its base in an isosceles triangle. Calculate its interior angles. - Ratio iso triangle
The ratio of the sides of an isosceles triangle is 7:6:7. Find the base angle to the nearest answer correct to 3 significant figures.
Two separate cuboids with different orientations are in space. Determine the angle between them, knowing the direction cosine matrix for each separate cuboid. u1=(0.62955056, 0.094432584, 0.77119944) u2=(0.14484653, 0.9208101, 0.36211633)Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
