Absolute value - practice problems - page 2 of 7
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 131
- Calculate: 80496
Calculate: |7 − 15| + |8| − |−13| − 1 = - GEOMETRIC MEANS alternating
Find the indicated number of geometric means between the pair of numbers. -32 and 4 [insert 2 means] Sequence:-32, _, _, 4 - Crosswind
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Sum of absolute values
Is it possible for |r| + |s| = |r+s|? If so, when?
- A parking
A parking garage has five levels below ground. Each level is the same height. Consider ground level to be 0. The depth of the fifth level of the parking garage is -118.5 ft. What is the depth of the first level of the parking garage? - Drill bit
Bill's 3/8-inch drill bit is missing and needed for a job. He can get by with drilling a smaller hole than 3/8-inch as long as it is as close to 3/8-inch as possible. Which of the following bits would be the best to use? A. 13/32 inch B. 23/64 inch C. 1/2 - Parabola with abs
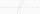A). Sketch the graph of the function f(x)=x * absolute(x) = x * |x| b). For what values of x is f(x) differentiable c). Find F(x) - Intersection 74914
Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis. - ABS, ARG, CONJ, RECIPROCAL
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
- Difference 73754
The difference between two positive integers is 25. One number is 59. What is the other number? - Calculate 71744
The triangle that connects on the dial: a) 2,7,9 b) 3,6,10 Calculate the size of the interior angles. - The temperature 30
The temperature in Hubby's office is 16 degrees Celsius, and the temperature outside his office is negative 7 degrees Celsius. What is the difference in temperature in these two places? - Unknown 63224
You will find an unknown number on the number line between 428 and the unknown number 290. - Vectors
Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6)
- Coordinates 59863 The endpoint of the vector, which is located at the origin of the Cartesian system Oxy, is given. Determine the coordinates of the vector and its magnitude, and sketch it: P[3,4]; Q[-2,7]; S[-5,-2] . .. i.e., Vectors PO, QO, SO
- Coordinate 59833
Determine the unknown coordinate of the vector so that the vectors are collinear: e = (7, -2), f = (-2, f2) c = (-3/7, c2), d = (- 4.0) - RS ABS
Find the distance between points R and S on a number line, with coordinates -4 and -7, respectively. - Displacement 55871
Assemble the two offsets, d1, and d2, shown by OA and OB oriented lines. The coordinates of the points are O = (0m, 0m), A = (3m, 3m), and B = (5m, 2m). Measure the magnitude of the resulting displacement d. - Ferdinand
Ferdinand went from place A to place B and from there to place C. A is 7.2 km from B, and B is 11.7 km from C. Albert went from place A to place D and from there to place C. D is 9.1 km from A and C is 10.8 km from D. Who traveled more and by how much?
Find the perimeter and the area of the polygon with the given vertices. T (2,7), U (2,9), V (5,9), W (5,7)Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
