The sum 47
The sum of 3 numbers in an arithmetic progression (AP) is 15. If 1,4,19 are to be added to the above numbers respectively, it formed a geometric progression (GP). Find the numbers.
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraplanimetryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Sequences AP + GP
The three numbers that make up the arithmetic sequence have the sum of 30. If we subtract from the first 5, the second 4, and keep the third, we get the geometric series. Find AP and GP members. - Find next member
Find x if the numbers from a GP are 7, 49, and x. - Three members GP
The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers. - Three Numbers GP
The sum of three Numbers in geometric progression (GP) is 38, and their product is 1728. Find the Numbers. - The block
The block, the edges formed by three consecutive GP members, has a surface area of 112 cm². The sum of the edges that pass through one vertex is 14 cm. Calculate the volume of this block. - Six terms GP
Find the sum of the six terms of the finite geometric sequence 96, -48, 24, -12 - The terms
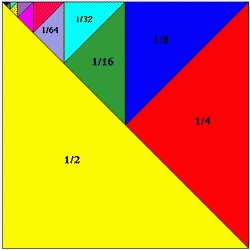
The terms 1/64, 1/32, and 1/16 form a geometric progression (GP). If the sum of the GP is (2³6 – 2-6), find the number of terms.
