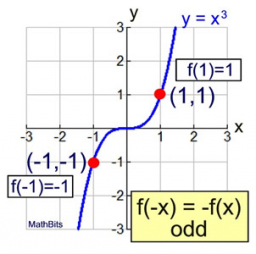
An odd function
If the points (5, -6) and (-3, 4) lie on the graph of an odd function f, then what are the values of f(-5) and f(3)? Is it possible to know this without seeing the graph of f?
We found some error in processing this page
We found some error in processing this page
Correct answer:
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Set of coordinates
Consider the following ordered pairs that represent a relation. {(–4, –7), (0, 6), (5, –3), (5, 2)} What can be concluded about the domain and range for this relation? A. The domain is the y values of the ordered pairs. B. The range is the set of output v - X-coordinate 81737
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - A Cartesian framework
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Parabola with abs
A). Sketch the graph of the function f(x)=x * absolute(x) = x * |x| b). For what values of x is f(x) differentiable c). Find F(x)
- The graph
Given that (-5,8) is on the graph of f(x), find the corresponding point for the function f(x)-2. - Bivariate data set
Here is a bivariate data set in which you believe y to be the response variable. x y 51.4 44.8 60.2 46.6 60.1 46.8 45.8 46.3 37.4 41.8 72.4 52.5 60 48.2 67.5 49.5 60.9 49.8 51.1 45.7 62.7 49.6 194.9 84.2 Make a scatter plot of this data. Which point is an - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a
