Hypotenuse 72524
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
Correct answer:
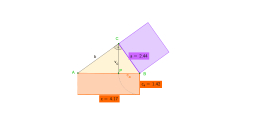
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert time units like minutes to seconds?
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- expression of a variable from the formula
- arithmetic
- square root
- planimetrics
- Pythagorean theorem
- The right triangle altitude theorem
- basic functions
- percentages
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Right-angled 82471
The lengths a = 7.2 cm and b = 10.4 cm are dropped in the right-angled triangle ABC. Do the math a) lengths of the sections of the hypotenuse b) height on the hypotenuse c - Right triangle ABC
Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse. - Euclid1
The right triangle ABC has hypotenuse c = 20 cm. How large sections cut height hc=9 cm on the hypotenuse c? - Trapezoid ABCD
Calculate the perimeter of trapezoid ABCD if we know the side c=12, b=19, which is also a height, and side d=32.
- Hypotenuse and height
In a right triangle is length of the hypotenuse c = 54 cm and height hc = 25 cm. Determine the length of both triangle legs. - RT triangle and height
Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm. - Median in right triangle
In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse).
