Deviation 70434
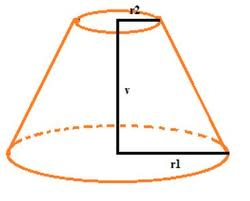
Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- surface area
- frustum
- planimetrics
- area of a shape
- triangle
- numbers
- fractions
- goniometry and trigonometry
- cosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Deviation 70744
Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30 ° from the base plane. - Calculate 32281
The rotating cone has a base radius r = 226mm, and the deviation of the side from the base plane is 56 °. Calculate the height of the cone. - Quadrangular pyramid
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =? - Angle of deviation
The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane.
- Top-open tank
The top-open tank resembles a truncated rotating cone, standing on a smaller base. Its volume is 465 m3, and the bases' radii are 4 m and 3 m. Find the tank's depth. - Consumption 69174
The tower's roof has the shape of the shell of a rotating cone with a base diameter of 4.3 m. The deviation of the side from the plane of the base is 36°. Calculate the consumption of sheet metal to cover the roof, assuming 8% for waste. - Frustrum - volume, area
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm.
