Equation + analytic geometry - practice problems - page 3 of 6
Number of problems found: 110
- Geometry: 78014
Good day, Even though it is a trivial task, I don’t know how to deal with it. This is analytic geometry: Find all integers a, b, and c such that the line given by the equation ax+by=c passes through the points [4,3] and [−2,1]. Thank you for your answer - Intersection 74914
Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis. - Equal distance
Find the equation for all the points (x, y) that are equal in distance from points A(5,-2) and B(-2,10). - A Ferris wheel
A Ferris wheel with a diameter of 100 feet makes five revolutions every 8 minutes. The base of the wheel is 4 feet above the ground. Your friend gets on at 3 PM sharp. a) Write an equation in seconds to express your friend's height in feet at any given ti
- Intersections 62784
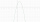A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3 - What is 19
What is the equation of the line whose x-intercept is - 3 and y-intercept is -4? Find coefficients A, B, C in normal line equation: Ax + By = C - Using
Using the point-slope equation, find the equation containing (-7, 3) and slope m = -4 - A circle
A circle relation is given to be x² + y² =16. What is the radius of the circle? - A Cartesian framework
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
- Parametric equation
Point A [6; -2]. Point B = [-3; 1] Write the parametric equation of the line BA so that t belongs to the closed interval < 0;3 > - Direction vector The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lie on the line p C) parametric equations
- General line equations In all examples, write the GENERAL EQUATION OF a line that is given in some way. A) the line is given parametrically: x = - 4 + 2p, y = 2 - 3p B) the slope form gives the line: y = 3x - 1 C) the line is given by two points: A [3; -3], B [-5; 2] D) the lin
- The tangent line
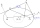Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1. - Tangents to ellipse Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1].
- There
There is a triangle ABC: A (-2,3), B (4, -1), C (2,5). Determine the general equations of the lines on which they lie: a) AB side, b) height to side c, c) Axis of the AB side, d) median ta to side a - Isosceles triangle
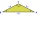In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Equation of the circle
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Points in space
There are n points, of which no three lie on one line and no four lies on one plane. How many planes can be guided by these points? How many planes are there if there are five times more than the given points? - Intersections 3
Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0
On a line p : 3 x - 4 y - 3 = 0, determine the point C equidistant from points A[4, 4] and B[7, 1].Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
