Fraction calculator
This fraction calculator performs all fraction operations - addition, subtraction, multiplication, division and evaluates expressions with fractions. It also shows detailed step-by-step information.
The result:
8 1/6/1 7/8 = 196/45 = 4 16/45 ≅ 4.3555556
The result spelled out in words is one hundred ninety-six forty-fifths (or four and sixteen forty-fifths).How do we solve fractions step by step?
- Conversion a mixed number 8 1/6 to a improper fraction: 8 1/6 = 8 1/6 = 8 · 6 + 1/6 = 48 + 1/6 = 49/6
To find a new numerator:
a) Multiply the whole number 8 by the denominator 6. Whole number 8 equally 8 * 6/6 = 48/6
b) Add the answer from the previous step 48 to the numerator 1. New numerator is 48 + 1 = 49
c) Write a previous answer (new numerator 49) over the denominator 6.
Eight and one sixth is forty-nine sixths. - Conversion a mixed number 1 7/8 to a improper fraction: 1 7/8 = 1 7/8 = 1 · 8 + 7/8 = 8 + 7/8 = 15/8
To find a new numerator:
a) Multiply the whole number 1 by the denominator 8. Whole number 1 equally 1 * 8/8 = 8/8
b) Add the answer from the previous step 8 to the numerator 7. New numerator is 8 + 7 = 15
c) Write a previous answer (new numerator 15) over the denominator 8.
One and seven eighths is fifteen eighths. - Divide: 49/6 : 15/8 = 49/6 · 8/15 = 49 · 8/6 · 15 = 392/90 = 2 · 196 /2 · 45 = 196/45
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 15/8 is 8/15) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the following intermediate step, cancel by a common factor of 2 gives 196/45.
In other words, forty-nine sixths divided by fifteen eighths equals one hundred ninety-six forty-fifths.
Rules for expressions with fractions:
Fractions - write a forward slash to separate the numerator and the denominator, i.e., for five-hundredths, enter 5/100. If you use mixed numbers, leave a space between the whole and fraction parts.Mixed numerals (mixed numbers or fractions) - keep one space between the whole part and fraction and use a forward slash to input fraction i.e., 1 2/3 . A negative mixed fraction write for example as -5 1/2.
A slash is both a sign for fraction line and division, use a colon (:) for division fractions i.e., 1/2 : 1/3.
Decimals (decimal numbers) enter with a decimal dot . and they are automatically converted to fractions - i.e. 1.45.
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| - | minus sign | subtraction | 1 1/2 - 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2/3 × 5/6 |
| : | division sign | division | 1/2 : 3 |
| / | division slash | division | 1/3 / 5 |
| : | colon | complex fraction | 1/2 : 1/3 |
| ^ | caret | exponentiation / power | 1/4^3 |
| () | parentheses | calculate expression inside first | -3/5 - (-1/4) |
Examples:
• adding fractions: 2/4 + 3/4• subtracting fractions: 2/3 - 1/2
• multiplying fractions: 7/8 * 3/9
• dividing Fractions: 1/2 : 3/4
• reciprocal of a fraction: 1 : 3/4
• square of a fraction: 2/3 ^ 2
• cube of a fraction: 2/3 ^ 3
• exponentiation of a fraction: 1/2 ^ 4
• fractional exponents: 16 ^ 1/2
• adding fractions and mixed numbers: 8/5 + 6 2/7
• dividing integer and fraction: 5 ÷ 1/2
• complex fractions: 5/8 : 2 2/3
• decimal to fraction: 0.625
• Fraction to Decimal: 1/4
• Fraction to Percent: 1/8 %
• comparing fractions: 1/4 2/3
• square root of a fraction: sqrt(1/16)
• expression with brackets: 1/3 * (1/2 - 3 3/8)
• compound fraction: 3/4 of 5/7
• fractions multiple: 2/3 of 3/5
• divide to find the quotient: 3/5÷2/3
The calculator follows well-known rules for the order of operations. The most common mnemonics for remembering this order are:
- PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.
- BEDMAS: Brackets, Exponents, Division, Multiplication, Addition, Subtraction.
- BODMAS: Brackets, Order (or "Of"), Division, Multiplication, Addition, Subtraction.
- GEMDAS: Grouping symbols (brackets: `(){}`), Exponents, Multiplication, Division, Addition, Subtraction.
- MDAS: Multiplication and Division (same precedence), Addition and Subtraction (same precedence). MDAS is a subset of PEMDAS.
1. Multiplication/Division vs. Addition/Subtraction: Always perform multiplication and division *before* addition and subtraction.
2. Left-to-Right Rule: Operators with the same precedence (e.g., `+` and `-`, or `*` and `/`) must be evaluated from left to right.
Fractions in word problems:
- Fraction multiplication
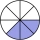 Solve six times three-sixths equals blank. Leave your answer as an improper fraction. thirty-six thirds eighteen-sixths eighteen-sixteenths three thirty-sixths
Solve six times three-sixths equals blank. Leave your answer as an improper fraction. thirty-six thirds eighteen-sixths eighteen-sixteenths three thirty-sixths - A student 4
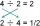 A student knows that ¾ x 4 is the same as 4 x ¾ The student assumes that 4 ÷ ¾ is the same as ¾ ÷ 4 Is the student correct?
A student knows that ¾ x 4 is the same as 4 x ¾ The student assumes that 4 ÷ ¾ is the same as ¾ ÷ 4 Is the student correct? - Simplest form of a fraction
 Which one of the following fractions is not equal to 3/2 after reducing to the simplest form? a) 15/20 b) 12/8 c) 27/18 d) 6/4
Which one of the following fractions is not equal to 3/2 after reducing to the simplest form? a) 15/20 b) 12/8 c) 27/18 d) 6/4 - Shandra
 Shandra saved $24. She lends 1/3 of her savings to her brother. Shandra wants to buy an $18 bracelet. Will she have enough money to purchase the bracelet? Explain
Shandra saved $24. She lends 1/3 of her savings to her brother. Shandra wants to buy an $18 bracelet. Will she have enough money to purchase the bracelet? Explain
- Three-quarters 47331
 A cylindrical container is three-quarters full with six liters of water. We dip a cube-shaped body into the container, which sinks to the bottom. The length of the edge of the cube is 13 cm. Decide what happens to the sink after the cube is dipped.
A cylindrical container is three-quarters full with six liters of water. We dip a cube-shaped body into the container, which sinks to the bottom. The length of the edge of the cube is 13 cm. Decide what happens to the sink after the cube is dipped. - Playing games
 In a school, 9/10 of the students take part. 2/3 of these play football. What fraction of the students play football?
In a school, 9/10 of the students take part. 2/3 of these play football. What fraction of the students play football? - An Airbus
 An Airbus A380 has one first-class section, one business-class section, and 4 economy-class sections. The first-class section of the Airbus A380 has 14 seats, 5/7 are being used. The business-class section has 64 seats. 5/16 is being used. Each Economy-cl
An Airbus A380 has one first-class section, one business-class section, and 4 economy-class sections. The first-class section of the Airbus A380 has 14 seats, 5/7 are being used. The business-class section has 64 seats. 5/16 is being used. Each Economy-cl
more math problems »
Last Modified: April 16, 2025
